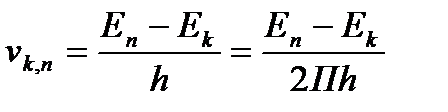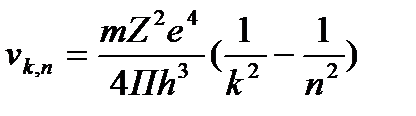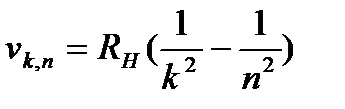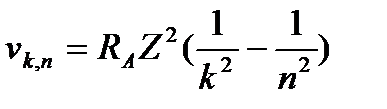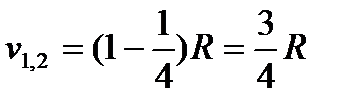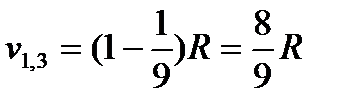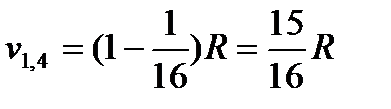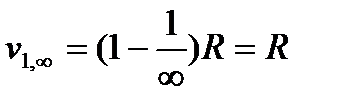Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Главное, орбитальное и магнитное квантовые числа. Квантование энергии электрона в атоме водорода.⇐ ПредыдущаяСтр 11 из 11 Электрон, движущийся по круговой орбите, обладает одной степенью свободы (угол поворота ф) и его состояние определяется одним квантовым числом п. Такое представление наглядно, но неверно. Т-функция представляет пространственную волну, соответствующую трем степеням свободы электрона. Пространственная волна определена в координатах радиуса г и двух углов ф и 0 и характеризуется тремя системами узловых поверхностей ( Главное квантовое число п определяет энергию электрона и номера слоев орбит (групп состояний) с разными значениями других квантовых чисел.
m=0, ±1, ± 2, ..., ± l, т.е. данному l отвечает всего 2l + 1 разных значений т. Величина т ограничена, так как проекция вектора момента не может превышать длины самого вектора. Величина и форма электронной волны  При слабой зависимости Е от l и т, считают, что каждый из уровней (49.13) при данном п расщепляется на ряд близких уровней. Каждому значению l соответствует 21 + 1 уровней с различными значениями (49.25) т. Общее число «орбит», отличающихся значениями I или т, при данном n.
Состояния движения электрона с разными моментами импульса имеют специальные названия. Если квантовое орбитальное число l равно нулю, то говорят, что электрон находится в s-состоянии, при l =1 — в p-состоянии и т. д. (табл.). Таблица Орбитальное число 01 2 3 4 Состояние s р d l g Говоря о р-состоянии, d-состоянии и т.д., имеют в виду состояния движения, в которых орбитальное квантовое число равно 1, 2 и т.д. При этом пользуются наглядным представлением об электроне как электронном облачке с распределенным зарядом плотностью -
Спектр атома водорода. Орбитальный и магнитный момент электрона. Собственный механический момент импульса электрона (спин). Спиновый магнитный момент электрона. Спиновое и магнитное спиновое квантовые числа. Принцип запрета Паули. Опыт Штерна и Герлаха. При переходе электрона с орбиты п на к, где п > к (при Еп > Ek) с излучением фотона, имеем: Еп - Ек = hv кп. Следовательно, Подставляя в это выражение значения Е, из (49.13), находим: В случае Z, отличного от единицы и при «постоянной Ридберга» RА с учетом конечного значения массы ядра (для водорода: RH = 3,28805 1015 с-1)
Фиксируя значение к и меняя п, имеем набор частот - «спектральную серию». При к = 1 и п = 2, 3, ... получаем частоты v1,2, v1,3; v1,4 и т. д., отвечающие переходу электрона со второго, третьего и т. д. слоев орбит на орбиту первого слоя. Фотоны этой серии Лаймана отнесены к ультрафиолетовой области спектра:
…………………. ………………….
При к = 2 и п = 3, 4, 5, получаем частоты второй серии Бальмера переходов электрона на вторую устойчивую орбиту. Линии этой серии лежат в ультрафиолетовой и видимой области. Частоты третьей и других серий лежат в инфракрасной области. Собственный механический момент электрона(спин). Спиновый магнитный момент электрона. Спиновое квантовое число. В 1925 г. Гаудсмит и Уленбек предположили, что электроны обладают собственными механическим и магнитным моментами. Представление электрона в виде вращающегося шарика, наглядно придает ему механический момент импульса. Отсюда название - спин (spin - веретено). Представление о вращении зарядов с круговым током и появлением магнитного момента оказалось не верно. Поэтому просто полагают внутренне присущие электрону собственные механический и магнитный моменты. К трем квантовым числам п, I и т, характеризующим «форму» орбиты и ее ориентацию в пространстве, добавляется спиновое квантовое число 5, характеризующее ориентацию собственных моментов электрона, принимая одно из двух значении ± 1/2, независимо от значении первой тройки квантовых чисел. Таким образом, число N„ различных состояний, отвечающих данному значению п, ока- зывается вдвое больше (см. (49.27)): Nn = 2п . При этом выполняется принцип Паули: никакие два электрона в атоме не могут обладать одинаковыми значениями всех четырех квантовых чисел (п, I, т, 5). Опыт Штерна и Герлаха. Явление, названное «пространственным квантованием», обнаружили экспериментально в 1922 г. Отто Штерн и Вальтер Герлах. В однородном магнитном поле на магнитный диполь действует момент сил, но результирующая сила равна нулю. При попадании в такое поле диполь будет ориентироваться по полю без изменения траектории. Если диполь переходит в неоднородное поле, то на его полюсы действуют разные силы с отличной от нуля результирующей. В таком поле траектория будет зависеть от направления его дипольного момента. Представляя атом магнитиком с магнитным моментом следует ожидать разное отклонение атомов с разными проекциями момента на направление магнитного поля. В опыте Штерна - Герлаха источником атомного пучка служила электропечь с веществом, подлежащим изучению. С помощью ряда диафрагм выделялся тонкий пучок атомов и пропускался сквозь магнитное поле с сильной неоднородностью, ощутимой на расстояниях порядка размеров атомов, т. е. 1 А. Этого удалось добиться с помощью магнитов с полюсными наконечниками. Далее поток осаждался на пластинке. Тонкий штрих (след атомарного пучка в отсутствие магнитного поля) при наличии мощного неоднородного поля расщеплялся. Литий, серебро, атомарный водород давали всегда двойной след. Согласно теории Шредин- гера, магнитный момент, обусловленный орбитальным движением электрона атома водорода, и каждого из трех электронов лития равен нулю. Так же равен нулю суммарный магнитный момент орбитального движения всех электронов атома серебра. Значит, расщепление в магнитном поле пучка атомов этих элементов можно объяснить только двумя возможными ориентациями спинового магнитного момента валентного электрона. Это подтвердило наличие спина электрона
|
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 704. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
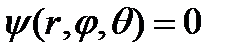 ), например: сферы постоянного радиуса r = const, конусы постоянного угла раствора
), например: сферы постоянного радиуса r = const, конусы постоянного угла раствора 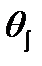 = const и плоскости
= const и плоскости 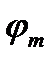 = const (рис. 23). Волновая функция и энергия электрона в поле ядра зависят от квантовых чисел п, / и т.
= const (рис. 23). Волновая функция и энергия электрона в поле ядра зависят от квантовых чисел п, / и т.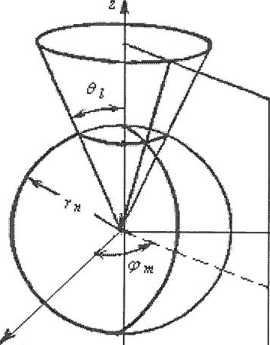 Азимутальное квантовое число / определяет величину момента импульса:
Азимутальное квантовое число / определяет величину момента импульса: 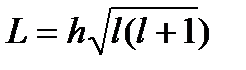
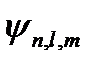 определяются значениями квантовых чисел п и l. Квантовое число т характеризует ориентацию орбиты в пространстве, задавая «пространственное квантование». При сферически симметричном электрическом поле энергия электрона может зависеть только от п и l, определяющих форму электронного облака, но не от т. Зависимость энергии от т возникает, если атом находится в магнитном поле.
определяются значениями квантовых чисел п и l. Квантовое число т характеризует ориентацию орбиты в пространстве, задавая «пространственное квантование». При сферически симметричном электрическом поле энергия электрона может зависеть только от п и l, определяющих форму электронного облака, но не от т. Зависимость энергии от т возникает, если атом находится в магнитном поле.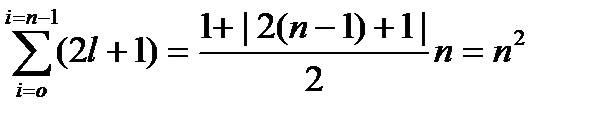
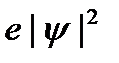 .
.