
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Частица в потенциальной яме. Прохождение частицы через потенциальный барьер. Квантовый гармонический осциллятор.Результирующая сила, действующая на свободный электрон (в металле) со стороны ионов и всех остальных электронов, равна нулю. Следовательно, потенциальная энергия электрона внутри металла постоянна, и ее удобно назначить Uвнутр = 0. На границах металла расположен двойной электрический слой, для преодоления которого нужно затратить работу выхода А. Поэтому потенциальная энергия электрона вне металла Uвнеш=A>0
 Потенциальным барьером называют область пространства, где потенциальная энергия больше, чем в окружающих областях пространства. В простейшем случае одномерного движения с потенциальным барьером прямоугольной формы (рис. 3) в областях I (-∞ < х < 0) и III (а < х < ∞) потенциальную энергию приравнивают нулю, тогда область II (0 <х< а) определена потенциальным барьером. Потенциальным барьером называют область пространства, где потенциальная энергия больше, чем в окружающих областях пространства. В простейшем случае одномерного движения с потенциальным барьером прямоугольной формы (рис. 3) в областях I (-∞ < х < 0) и III (а < х < ∞) потенциальную энергию приравнивают нулю, тогда область II (0 <х< а) определена потенциальным барьером.
 Гармонический осциллятор массой т обладает кинетической и потенциальной энергией. Для одномерного осциллятора потенциальная энергия (рис.19) U(х) = (1/2)kx2, кинетическая энергия К = (p2)/(2m). В классической механике такой осциллятор совершает гармонические колебания с собственной частотой. Амплитуда колебаний А и полная энергия E ~ A2 могут принимать любые значения от 0 до ∞.
(48.43) В результате решения уравнения (48.43) энергия осциллятора может принимать лишь дискретные значения (рис. 19 пунктир) (48.45)
Вид волновых функций ψ0, ψ1 и ψ2 для первых трех значений энергии приведен на рис. 17. Минимальная энергия осциллятора не равна нулю:E0= (1/2)hν (48.46) а все энергетические ступеньки имеют одну высоту Квантовый осциллятор в стационарном состоянии ничего не излучает. Излучение возникает при переходе осциллятора из данного энергетического состояния в ближайшее нижнее одним единственным фотоном. Это же относится и к поглощению излучения.
|
|||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 816. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 Поместим начало координат 0 в центр бруска металла длиной l и направим ось x перпендикулярно его границам. Потенциальная энергия U(x) (рис. 15). Пока кинетическая энергия электрона в металле мала по сравнению с высотой стенок «потенциальной ямы» (Екин <<А) электронные волны испытывают на границах полное внутреннее отражение.
Поместим начало координат 0 в центр бруска металла длиной l и направим ось x перпендикулярно его границам. Потенциальная энергия U(x) (рис. 15). Пока кинетическая энергия электрона в металле мала по сравнению с высотой стенок «потенциальной ямы» (Екин <<А) электронные волны испытывают на границах полное внутреннее отражение.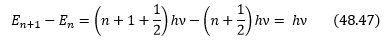 Если частица с энергией Е движется в области I по направлению потенциального барьера, то при Е < U0 она не сможет его преодолеть и отразится, изменив направление движения на обратное. В случае Е > U0 частица преодолеет потенциальный барьер и попадет в область III, где будет продолжать двигаться с прежней энергией в положительном направлении оси X. В рамках квантовой механики в случае Е < U0 существует вероятность проникновения частицы через потенциальный барьер из области I в область III (туннельный эффект), а для Е > U0 существует определенная вероятность ее отражения.
Если частица с энергией Е движется в области I по направлению потенциального барьера, то при Е < U0 она не сможет его преодолеть и отразится, изменив направление движения на обратное. В случае Е > U0 частица преодолеет потенциальный барьер и попадет в область III, где будет продолжать двигаться с прежней энергией в положительном направлении оси X. В рамках квантовой механики в случае Е < U0 существует вероятность проникновения частицы через потенциальный барьер из области I в область III (туннельный эффект), а для Е > U0 существует определенная вероятность ее отражения. В квантовой механике ψ-функция и возможные значения энергии определяются из уравнения Шредингера
В квантовой механике ψ-функция и возможные значения энергии определяются из уравнения Шредингера