
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принцип неопределенностей. Соотношение неопределенностей.Уравнения В том же одномерном представлении волна' любой природы (акустическая, электромагнитная, волна де Бройля), характеризуется волновой функцией Ψ (плотность и давление в акустической волне или векторы Е и Н в электромагнитной волне). Значения величины у различны в точках с разными ко-ординатами х и меняются с течением времени t, т. е. Ψ = Ψ(х, t). Простейшая монохроматическая волна, распространяющаяся вдоль оси ОХ,описывается волновой функцией
 Для того чтобы волновая функция была отлична отнуля внутри интервала ∆х и практически равнялась нулювне его, она должна представляться суперпозицией монохроматических волн (46.4) разных амплитуд и с разными длинами в интервале от 𝛌 до 𝛌+ ∆𝛌 (рис 13, а). Результат их сложения - волновой пакет (рис. 13, б), представляющий набор монохроматических волн, с возможными значениями импульса в интервале ∆р = ∆ Если положение электрона в данный момент времени определено в пространстве (бесконечно узкий волновой пакет), то в силу неопределенности импульсаэтого пакета его положение в следующий момент времени не однозначно. Поэтому и траектория движения электрона имеет приближенное понятие. Координата иимпульс дополнительны друг другу, т.к. не определены одновременно. По одному из мысленных опытов Гейзенберга для определения положения иимпульса электрона, его нужно «осветить» и получить хотя бы один рассеянный при столкновении фотон. Вследствие дифракции, точность в определении координаты электрона не может быть больше длины волны излучения: ∆х ≈ 𝛌. Чем точнее нужно измерить положение электрона, тем меньше должно быть 𝛌. Но при рассеянии фотона электрон получает отдачу и его импульс меняется на величину ∆рх порядка импульса фотона: рф = h/𝛌 что составит погрешность в определенииего импульса. Получаем «соотношением неопределенностей»: ∆х∆рх
Рассмотрим движение электрона в электроннолучевой трубке. Пусть неопределенность импульса в волновом пакете не превышает 1 % (∆p≈0,01p). Из (46.8) следует, что электрон в каждый данный момент локализован в области ∆х Бор показал, что аналогичное соотношение существует и для произведения неопределенности энергии ∆Е и неопределенности времени взаимодействия ∆t объекта с измерительным прибором, т.е. ∆E∆t > h.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 706. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =Fx и
=Fx и  =
=  pxпредставляют собой математическую формулировку принципа причинности в классической механике: если известны силы Fx, действующие на материальную точку, то из (46.2) можно определить приращения ее координаты (dx) и импульса (dpx в последовательные промежутки времени (dt) и тем самым рассчитать ее движение. Материальная точка, обладая одновременно определенными значениями координаты х и импульса рх, образует траекторию движения по совокупности своих последовательных положений в пространстве.
pxпредставляют собой математическую формулировку принципа причинности в классической механике: если известны силы Fx, действующие на материальную точку, то из (46.2) можно определить приращения ее координаты (dx) и импульса (dpx в последовательные промежутки времени (dt) и тем самым рассчитать ее движение. Материальная точка, обладая одновременно определенными значениями координаты х и импульса рх, образует траекторию движения по совокупности своих последовательных положений в пространстве. где 𝛌 - длина волны, а v - скорость ее распространения. Намгновенном снимке отрезка такой волны (рис. 12) пунктиром показан тот же отрезок волны спустя некоторый промежуток времени. Интервал координат ∆х, в котором заключен волновой объект, равен бесконечности.
где 𝛌 - длина волны, а v - скорость ее распространения. Намгновенном снимке отрезка такой волны (рис. 12) пунктиром показан тот же отрезок волны спустя некоторый промежуток времени. Интервал координат ∆х, в котором заключен волновой объект, равен бесконечности. Для электромагнитных и электронных волн импульс частицы (фотона и электрона, соответственно) р = h/𝛌. Так как монохроматической волне (𝛌 = const) отвечает определенное значение импульса частицы р, и интервал ∆р. Монохроматическая волна представляет объект с определенным импульсом и неограниченной областью локализации:∆х =
Для электромагнитных и электронных волн импульс частицы (фотона и электрона, соответственно) р = h/𝛌. Так как монохроматической волне (𝛌 = const) отвечает определенное значение импульса частицы р, и интервал ∆р. Монохроматическая волна представляет объект с определенным импульсом и неограниченной областью локализации:∆х =  и ∆р = 0, (46.6)
и ∆р = 0, (46.6) =
=  . Чем в более узком интервале ∆х локализована (отлична от нуля) результирующая волновая функция Ψ тем более широкий интервал длин интерферирующих волн ∆𝛌, входит в волновой пакет. Увеличение определенности влокализации волны (уменьшение ∆х) связано с одновременным возрастанием неопределенности импульса ∆р. В пределе имеем ∆х = 0 ∆р→
. Чем в более узком интервале ∆х локализована (отлична от нуля) результирующая волновая функция Ψ тем более широкий интервал длин интерферирующих волн ∆𝛌, входит в волновой пакет. Увеличение определенности влокализации волны (уменьшение ∆х) связано с одновременным возрастанием неопределенности импульса ∆р. В пределе имеем ∆х = 0 ∆р→ 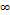 . (46.7) (46.7)
. (46.7) (46.7) 𝛌
𝛌  = h. То же имеет место и для других координатных осей:
= h. То же имеет место и для других координатных осей: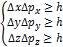 Положение волнового пакета характеризуется областью занимаемого им пространства с размерами ∆х, ∆у и ∆z. Точно так же ∆рх, ∆ру и ∆рz характеризуют спектральный состав монохроматических волн, представляющих волновой пакет. Никакой «неопределенности» нет, а «соотношения неопределенностей» Гейзенберга (46.8) характеризуют корпускулярно-волновую двойственность частицы.
Положение волнового пакета характеризуется областью занимаемого им пространства с размерами ∆х, ∆у и ∆z. Точно так же ∆рх, ∆ру и ∆рz характеризуют спектральный состав монохроматических волн, представляющих волновой пакет. Никакой «неопределенности» нет, а «соотношения неопределенностей» Гейзенберга (46.8) характеризуют корпускулярно-волновую двойственность частицы. 100𝛌. При υ = 10 м/с, длине волны электрона 𝛌= h/p ≈10-9м, область локализации ∆х≈10 -7 м, что во много раз меньше размеров трубки. Тогда по отношению к прибору разумным приближением является электрон - материальная точка. Представление же об электроне-корпускуле в атоме бессмысленно.
100𝛌. При υ = 10 м/с, длине волны электрона 𝛌= h/p ≈10-9м, область локализации ∆х≈10 -7 м, что во много раз меньше размеров трубки. Тогда по отношению к прибору разумным приближением является электрон - материальная точка. Представление же об электроне-корпускуле в атоме бессмысленно.