Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Нестационарное уравнение Шредингера. Стационарное уравнение Шредингера.Нестационарное уравнение Шредингера. В 1926 г. Шредингер нашел уравнение для ψ-функции электрона, не в свободном пространстве, а во внешнем поле. Пусть частица движется вдоль оси х с точно определенным импульсом рх - р. Частица не локализована и описывается монохроматической волной с фазой φ = 2π(vt - х/λ). С учетом Е = hv и р- h/λ преобразуем это выражение к виду φ =
Продифференцируем ψ-функцию по координате х:
Динамические переменные по известной ψ-функции определяются особым подходом: каждой динамической переменной сопоставляется определенная математическая операция над ψ-функцией. Если применить к волновой ψ-функции математическую операцию Уравнение (47.5) в принятых обозначениях:
Операторы по составляющим импульса по осям у и z, имеют вид
Применим один из этих операторов к Ψ -функции (47.4):
Рассматриваемая Ψ-функция описывает состояние, в котором составляющие импульса имеют значения: рх = р, ру = 0, pz = 0. Ψ-функцию (47.4) состояния с определенным значением импульса рх, называют собственной функцией импульса, а величину импульса в этом состоянии рх=p~ его собственным значением. В поиске оператора энергии продифференцируем функцию (47.4) по времени Сопоставляя полученное равенство с (47.5), находим: Полная энергия состоит из суммы кинетической и потенциальной энергий: Примечание: квадрат оператора рх означает последовательное применение обоих операторов к одной и той же функции:  Т.О., оператор кинетической энергии приобретает вид
Где Потенциальная энергия U (x,y,z) содержит только координаты, но не импульсы. Поэтому оператор потенциальной энергии U есть просто умножение на функцию U (x,y,z). Тогда оператор полной энергии (оператор Гамильтона):
Применение к волновой функции
Уравнение Шредингера в развернутом виде: {-
с помощью которого отыскивается волновая функция Ψ(х, у, z, t) частицы, позволяет найти
Стационарное уравнение Шредингера.В стационарном состоянии энергия Е частицы неизменна во времени. Это значит, что волновая функция ψ должна быть собственной функцией оператора энергии E^ и применение этого оператора эквивалентно умножению у на постоянный множитель Е, т. е.
и уравнение Шредингера для стационарных состояний имеет вид
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 862. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (Et — px) =
(Et — px) = 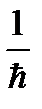 (Et — px).
(Et — px). ψ-функция комплексная, вида:
ψ-функция комплексная, вида: и
и  (47.5)
(47.5)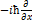 , то значение динамической переменной рх = р получится в виде множителя при ψ. Представляющий динамическую переменную рх оператор
, то значение динамической переменной рх = р получится в виде множителя при ψ. Представляющий динамическую переменную рх оператор  (47.6)
(47.6)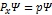 (47.7)
(47.7)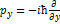 и
и 
 аналогично
аналогично 
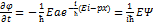

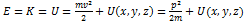 где
где 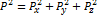
 (-iћ
(-iћ 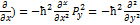 ;
; 
 (
(  ∆
∆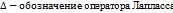 ∆=(
∆=( 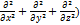
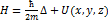 . (47.19)
. (47.19)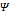 оператора 47.19 дает тот же результат, что и применение оператора (47.14), а именно
оператора 47.19 дает тот же результат, что и применение оператора (47.14), а именно
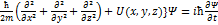 (47.21)
(47.21)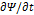 в заданном внешнем поле.
в заданном внешнем поле.