
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модель атома Резерфорда. Постулаты Бора. Теория водородоподобного атома Бора.Модель атома Резерфорда. До конца XIX в. господствовало убеждение, что атомы, как мельчайшие частицы химически простых тел, являются неделимыми частицами материи. Движение материи понималось как механическое перемещение этих частиц. Изменение химического состава сложных веществ представлялось взаимным замещением атомов, переходящих от одних молекулярных соединений к другим. И вот при электрическом разряде в газе были обнаружены катодные лучи - отрицательно заряженных частиц, названных электронами. Было установлено, что электроны вырываются из атомов, которые при этом становятся положительно заряженными ионами. Стало очевидным, что во всех атомах имеются одинаковые по свойствам электроны, и что нейтральные атомы являются системами электрически заряженных частиц. Измерения удельного заряда (q/m) электронов показали, что масса электрона в тысячи раз меньше массы атомов. Положительный заряд оказался связанным с основной массой атома. Д.Д. Томсон (1910 г.) предложил первую «модель» атома в форме сферы, равномерно наполненной положительно заряженной материей, в которой движутся отрицательно заряженные электроны. Модель дает одну линию на спектре. Гейгер и Марсден, исследовали рассеяние -частиц в металлической фольге. Преимущество -частиц как инструмента в исследовании структуры атома - в их высокой монохроматичности (𝑎-частицы, вылетающие из атомов данного сорта, имеют практически одну и ту же скорость). При большой массе -частицы не отклонялись при столкновениях с электронами атомов, и по их рассеянию в веществе можно было судить о распределении положительно заряженной материи. После прохождения фольги рассеянные -частицы регистрировались по вспышкам света (сцинтилляциям) на малом экране объектива микроскопа, покрытом флуоресцирующим веществом. Почти все -частицы отклонялись после прохождения фольги на небольшой угол 2 - 3°. На угол, превышающий 90°, рассеивалась примерно одна из 2*104 частиц, но некоторые (0,01 %), отклонялись на 180°. Резерфорд заключил, что отклонение на большой угол происходит в результате однократного взаимодействия 𝑎-частицы с положительным зарядом большой массы, заключенной в малом объеме. Он предложил «ядерную» модель атома, по которой центре атома находится положительно заряженное «ядро» с массой почти равной массе атома. Вокруг ядра под действием электрических сил движутся электроны. Так как кулоновские силы убывают с расстоянием по тому же закону, что и силы ньютоновского тяготения (как 1/г ), то атом становился подобным солнечной планетарной системе. Так как атомы нейтральны, то при заряде ядра Ze вокруг ядра должно двигаться Z электронов. Но и эта модель оказалась неудовлетворительной. Так как любому значению радиуса орбиты r соответствует определенная скорость о и энергия Е электрона на данной орбите, то при бесчисленных орбитах на различных расстояниях от ядра величины r, v и Е могут меняться непрерывно. Тогда при переходе с одной орбиты на другую может испускаться любая порция энергии, и спектры атомов должны быть непрерывными.  Механически устойчивая модель Резерфорда оказалась неустойчивой с точки зрения законов классической электродинамики. Электроны, движущиеся по круговым орбитам, обладают нормальным ускорением. При радиусе орбиты r =10-10м ускорение равно 10 м/с . При таких ускорениях электроны должны интенсивно излучать электромагнитные волны, быстро теряя энергию, приближаясь к ядру. Такой атом не мог существовать более 10-6 с. Постулаты Бора. Нильс Бор применил квантовую теорию Эйнштейна к атому. Он исходил из опытного факта: атомы, как элементарные излучатели, отдают излучение в виде порций ε= hv. Возможные состояния атома характеризуются последовательностью по дискретному ряду Е1 Е2, ..., Еп энергии атома. Находясь в одном из таких, «разрешенных» состояний, атом не испускает и не поглощает излучения, и его энергия не меняется. Изменение состояния (энергии) атома может происходит скачком от одного состояния к другому. Первый постулат Бора устанавливает связь между возможными значениями энергии Ек и Еi атома и частотами vik испускаемого (поглощаемого) излучения: hvik= Ek - Ei (44.3) Откуда получалось, что на разрешенных круговых орбитах атома водорода момент импульса электрона mvr должен быть равен целому числу ћ=h/2п. Это позволило Бору записать постулат в форме правила для нахождения энергий разрешенных состояний атома для модели Резерфорда: Mvr = nћ(п= 1,2,3,...) Выделение малого числа разрешенных условием орбит и устойчивое движение заряженной корпускулы по круговой орбите исключаются законами классической механики и электродинамики, соответственно. Опыт Франка-Герца. При абсолютно упругих столкновениях кинетическая энергия и суммарный импульс сталкивающихся частиц остаются неизменными. При неупругом столкновении электрона с атомом внутренняя энергия атома может увеличиться за счет кинетической энергии сталкивающихся частиц. Относительная скорость частиц после столкновения станет меньше, чем до него. Такие удары принято называть ударами первого рода. Может иметь место и обратное явление, если внутренняя энергия атома до удара не является минимальной (атом возбужден). При столкновении с электроном такой атом может не только сохранить или увеличить внутреннюю энергию, но и уменьшить ее. Относительная скорость и суммарная кинетическая энергия частиц после удара возрастут за счет внутренней энергия атома. Такие удары называют ударами второго рода. Пусть атомы одноатомного газа находятся на энергетических уровнях: Е1 (наинизший), Е2,Е3, ... . Энергия теплового движения мала для возбуждения атомов: ЗкТ/2<<Е2 – Е1 и атомы находятся в невозбужденном состоянии с Е1.
движения электронов, но не энергию. Как только кинетическая энергия электронов г превысит Е2 — Е1 станут возможны удары первого рода. При этом кинетическая энергия атома практически не изменится, а внутренняя возрастет на величину Е2 – Е1. Энергия электрона ε уменьшится на эту же величину и станет έ́ =ε - (Е2 – Е1). Если ε< 2(Е2—Е1), дальнейшая потеря энергии электронами невозможна. Если ε> 2(Е2—Е1), то электрон может испытать два неупругих соударения и т. д. На рис. 7 показана схема опыта. Электроны, эмитируемые раскаленным катодом К, ускоряются между К и сеткой С1. В пространстве между С1 и С2 электрическое поле отсутствует и электроны движутся, испытывая соударения с атомами ртути, парами которой (при давлении 1 мм рт. ст.) наполнен объем. Часть электронов диффундирует через сетку С2 и, преодолевая задерживающий потенциал (0,5 В), падает на пластинку Р, соединенную через гальванометр G с землей.
Рассмотрим график энергетических уровней электронов в атоме водорода (рис. 9). Частоты излучения, возникающего при переходе электрона на основной, невозбужденный уровень Е1 других, более высоких, образуют первую серию частот в спектре испускания. Возможные переходы на следующий уровень Е2 порождают вторую серию, на Е3 - третью серию и т. д. Отметим у частоты v первым индексом номер серии, вторым — номер уровня, с которого совершил переход электрон при испускании фотона данной частоты: для частоты первой серии, возникшей при переходе Е5 →Е1 имеем hv1;5 = Е5 – Е1; для фотона третьей серии перехода Е6 →Е3, имеем hν3;6= Е6 - Е3 и hνnk=Ек-Еп Выпишем значения всех частот первой стадии:
Возьмем разность любых двух частот этого ряда, вычтя из большей - меньшую. Тогда при к > п имеем: ν1,k- ν1,n= Разность двух частот первой серии дает частоту одной из следующих серий: вычитая из ν1,2 последовательно, ν1,3,ν1,4 получаем частоты второй серии; вычитая из ν1,3 частоты ν1,4, ν1,6, ..., получаем третью серию и т.д. Таким же образом разности частот, скажем, третьей серии дадут частоты последующих: четвертой, пятой и других серий и т. д. (комбинационный принцип Ритца). Разным вариантам переходов отвечают определенные фотоны, и в спектрах они наблюдаются, но разной интенсивности. То, что некоторых фотонов испускается больше, указывает на предпочтительность определенных переходов. Порядок и причина переходов оставался не ясным.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 522. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
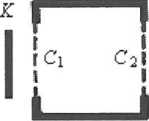 В газ впускается пучок электронов с одинаковой для всех электронов энергией ε < Е2 — Е1. Масса атома превышает массу электрона в тысячи раз, поэтому при упругом соударении электрона с атомом скорости атома и электрона не меняются. Таким образом, если энергетический спектр атомов дискретен, то соударения электронов с энергией ε < Е2 – Е1 с атомами могут изменить лишь направление
В газ впускается пучок электронов с одинаковой для всех электронов энергией ε < Е2 — Е1. Масса атома превышает массу электрона в тысячи раз, поэтому при упругом соударении электрона с атомом скорости атома и электрона не меняются. Таким образом, если энергетический спектр атомов дискретен, то соударения электронов с энергией ε < Е2 – Е1 с атомами могут изменить лишь направление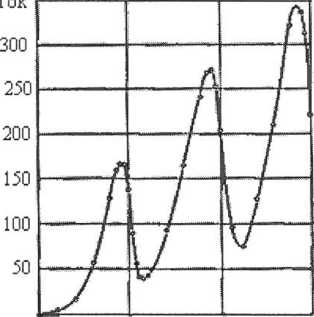 На графике зависимости тока в G как функции начальной энергии электронов 8, эВ (рис. 8) пики кривой тока кратны 4,9 эВ, что составляет энергию возбуждения (Е2—Е1) атомов ртути. Концепция дискретных энергетических уровней атома подтвердилась.
На графике зависимости тока в G как функции начальной энергии электронов 8, эВ (рис. 8) пики кривой тока кратны 4,9 эВ, что составляет энергию возбуждения (Е2—Е1) атомов ртути. Концепция дискретных энергетических уровней атома подтвердилась.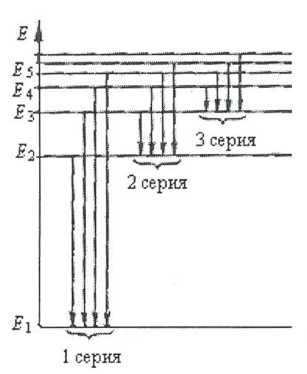 ν1,2=
ν1,2= 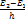 , ν1,3=
, ν1,3= 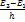 ,….., ν1,k=
,….., ν1,k= 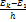 ,…
,…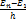 =
= 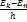 =νn,k
=νn,k