
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи для самостоятельного решения1. Найдите значение выражения:
2. Решите уравнение: 3. Сколько необходимо взять элементов, чтобы число размещений из них по четыре было в 14 раз больше, чем число размещений из (n−2) по три? 4. Сколько различных шестизначных чисел можно написать при помощи цифр 1, 2, 3, 4, 5, 6, 7, 8? Цифры в записи чисел не повторяются. 5. Клавиатура пианино состоит из восьмидесяти восьми клавиш. Сколько различных музыкальных фраз можно составить из шести нот, если не допускать в одной фразе повторения звуков? 6. Сколько всевозможных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5? Цифры в записи числа не повторяются. 7. В классе 12 свободных мест. Сколькими способами можно рассадить на них пять учеников? 8. В классе тридцать учащихся. Сколькими способами можно выбрать из класса команду из четырех учащихся, для участия в олимпиаде по обществознанию, русской литературе, математике и английскому языку? 9. Учащиеся девятого класса изучают двенадцать предметов. Сколькими способами можно составить расписание уроков на один день так, чтобы было шесть различных уроков? 10. Сколько нужно иметь различных словарей, чтобы непосредственно выполнять переводы с любого из шести языков (русского, английского, немецкого, французского, итальянского и испанского) на любой другой из этих языков? На сколько больше нужно иметь словарей, если к перечисленным языкам добавятся еще польский, португальский и шведский языки? 11. В шахматном турнире участвуют пять школьников и 15 студентов. Сколькими способами можно распределить места, занятые в турнире школьниками, если известно, что никто из участников не набрал одинакового количества очков? Сколькими способами можно распределить призовые места, если известно, что никто из участников не набрал одинакового количества очков?  12. Сколько различных шестизначных чисел можно написать при помощи цифр 0,1, 2, 3, 4, 5, 6, 7, 8, 9? Цифры в записи чисел не повторяются. 13. Труппа театра состоит из т актеров. Известно, что четырех претендентов на ведущие роли в пьесе можно выбрать числом способов в 56 раз большим, чем выбрать из этой же труппы двух претендентов на главные роли. Сколько артистов в труппе? Сочетания без повторений Термин «сочетание» в его современном значении начал первым употреблять Б. Паскаль. Обозначение C При составлении k – элементных подмножеств n–элементного множества нас не интересует порядок, в котором располагаются элементы. Например, если имеется 10 сортов ткани и нужно выбрать 4 сорта, то порядок, в котором будут выбраны сорта, не имеет значения. В таких задачах речь идёт о подмножествах, не являющихся упорядоченными. Определение. Всякое k-элементное подмножество n-элементного множества (k Число различных сочетаний из n элементов по k обозначают символом C Как следует из определения, 2 сочетания считают различными, если они отличаются друг от друга хотя бы одним элементом. Порядок следования элементов в сочетании значения не имеет. Теорема 8. Число сочетаний из n элементов по k элементов определяется по формуле:C ÿ Формула для числа сочетаний легко получается из формул для числа размещений и числа перестановок. Действительно, составив сначала все сочетания из n элементов по k, а затем, переставив всеми возможными способами элементы, входящие в каждое сочетание, получим все размещения из n–элементов по k–элементов. Но из каждого такого сочетания можно составить k! перестановок. То есть справедлива формула: k! C Теорема 8 доказана. Задача. Из группы студентов, состоящей из 25 человек, надо составить команду из 4 человек для участия в беге на 1000 м. Сколькими способами можно это сделать? Решение. Порядок следования элементов в данном соединении значения не имеет. Из 25 человек набрать команду из 4 человек можно: С Ответ: 12650 способов. Вспомним теорему о том, что конечное множество, содержащее п элементов, имеет 2п подмножеств, то есть если Ап={а1,а2,...,aп }, то п(Р(Ап))=2п. Напомним также, что принято считать 0! равным 1. При этом предположении формула С
Свойства чисел C Следующие простые свойства чисел С а) б) в) г) д) Правило симметрии. Если 0 Известно, что C Найдём C Следовательно, C Утверждение доказано. е) Для (n + 1) C (n + 1) C (k + 1)C Следовательно, (n + 1) C Утверждение доказано. ж) Правило Паскаля. Найдем C C Найдем C Найдём C C = з) Для любого m верны равенства: C C C Покажем, как данные свойства можно использовать при решении задач. Задача 1. Некоторый комитет состоит из 12 человек. Минимальный кворум для принятия решения должен насчитывать 8 человек. а) Сколькими способами может быть достигнут минимальный кворум? б) Сколькими способами может быть достигнут какой-либо кворум? Решение. а) Искомое число совпадает с С С б) Какой-либо кворум достигается, если на заседании присутствует 8, 9, 10, 11 или 12 членов комитета. Согласно правилу суммы искомое число равно: C =495 + (При вычислении мы учли, что 0!=1, и поэтому C Ответ: а) 495 способов; б) 794 способа. Задача 2. У 6 взрослых и 11 детей обнаружены признаки инфекционного заболевания. Сколькими способами можно взять выборочный анализ, чтоб изучить течение болезни у 2 взрослых и 3 детей. Решение. Из 6 взрослых выбрать двух можно: C Из 11 детей выбрать трёх можно: С Согласно правилу произведения имеется 15 ∙ 165=2 475 способов выбора двух взрослых и трёх детей. Ответ: 2 475 способов. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 663. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
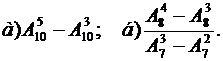
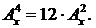
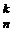 введено в 1880 году первоначально в виде
введено в 1880 году первоначально в виде 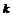 С
С 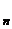 . Второе, принятое в настоящее время обозначение введено Л. Эйлером.
. Второе, принятое в настоящее время обозначение введено Л. Эйлером.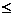 n) называют сочетанием без повторений из n элементов по k.
n) называют сочетанием без повторений из n элементов по k.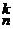 .
.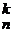 =
= 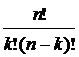 .
.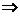 C
C 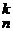 =
= 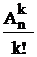 =
= 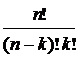 .
.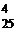 =
= 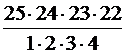 =12650 (способами).
=12650 (способами).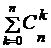 =2
=2 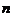 .
.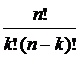 :
: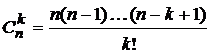 ;
;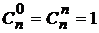 ;
;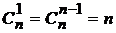 ;
;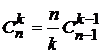 .
.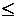 k
k 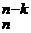 =C
=C 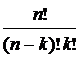 .
.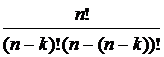 =
= 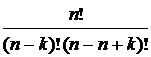 =
= 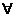 k,n: 0
k,n: 0 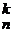 =(k + 1) C
=(k + 1) C 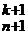 .
.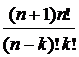 =
= 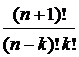 ;
;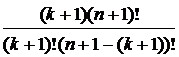 =
= 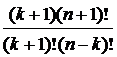 =
= 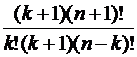 = =
= = 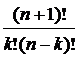 .
.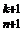 .
.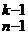 + C
+ C 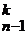 .
.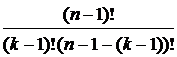 =
= 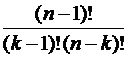
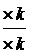 =
= 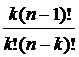 ;
;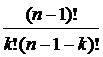 =
= 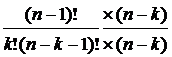 =
= 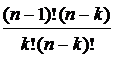 .
.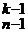 + C
+ C 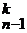 =
= 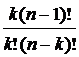 +
+ 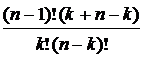 =
=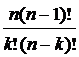 =
= 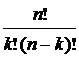 = C
= C 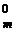 + C
+ C 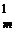 + … + C
+ … + C 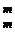 =2
=2 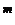 ;
;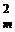 – C
– C 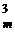 +…+ (– 1)
+…+ (– 1) 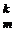 + … + (–1)
+ … + (–1) 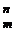 =0;
=0; + C
+ C 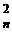 + C
+ C 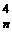 + …=C
+ …=C 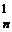 + C
+ C 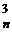 + C
+ C 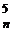 + …=2
+ …=2 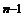 .
.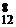 и равно:
и равно: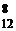 =С
=С 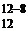 =С
=С 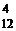 =
= 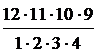 =495 (способа)
=495 (способа)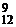 + C
+ C 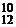 + C
+ C 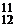 + C
+ C 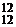 =C
=C 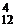 + C
+ C 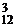 + C
+ C 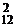 + C
+ C 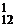 + C
+ C 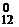 =
=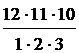 +
+ 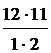 +
+ 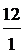 + 1=794 (способа )
+ 1=794 (способа )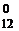 =1).
=1).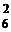 =
= 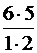 =15 (способами)
=15 (способами)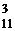 =
= 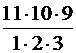 =165 (способами)
=165 (способами)