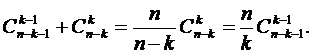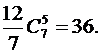Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи для самостоятельного решения1. Запишите формулу бинома Ньютона: 1) 5) 2. Выпишите п–й член бинома, если: а) п=4, а б) п=6, а в) п=5, а г) п=3, а Вопросы для самопроверки 1. Что называют «размещением с повторениями из k элементов по m? элементов»? 2. Как найти число размещений с повторениями из n элементов по k? 3. Докажите, что 4. Что называют«сочетанием с повторениями из n элементов по k»? 5. Как найти число сочетаний с повторениями из n элементов по k? 6. Докажите, что число сочетаний из n элементов по k элементов определяется по формуле:
7. Что называют «перестановками с повторениями из k элементов по m элементов»? 8. Как найти число перестановок с повторениями из n элементов по k? 9. Докажите, что 10. Что значит слово «бином»? Что такое треугольник Паскаля? 11. Запишите формулу бинома Ньютона. 12. Какие свойства биномиальных коэффициентов вы знаете?
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что такое комбинаторика? Какие задачи называют «комбинаторными»? 2. Докажите что, для любых множеств А и В справедливо равенства: B=(A 3. Чему равно число элементов объединения двух непересекающихся множеств? 4. Чему равно число элементов объединения двух произвольных конечных множеств? 5. Чему равно число элементов объединения трех пересекающихся множеств? 6. Сформулируйте комбинаторные правила суммы и произведения. 7. Дайте определение п!. 8. Дайте определение размещений без повторений из п элементов по k элементов. Приведите примеры. Чему равно число размещений без повторений из п элементов по k элементов? 9. Дайте определение сочетаний без повторений из п элементов по k элементов. Приведите примеры. Чему равно число сочетаний без повторений из п элементов по k элементов?  10. Дайте определение перестановок без повторений из п элементов. Чему равно число таких перестановок? 11. Дайте определение размещений с повторениями из п элементов по k элементов. Приведите примеры. Чему равно число размещений с повторениями из п элементов по k? 12. Дайте определение сочетаний с повторениями из п элементов по k элементов. Приведите примеры. Чему равно число сочетаний с повторениями из п элементов по k? 13. Дайте определение перестановок с повторениями данного состава. Приведите примеры. Чему равно число таких перестановок? 14. Какие свойства сочетаний вы знаете? Докажите их. 15. Какие свойства биномиальных коэффициентов вы знаете? Что вы знаете о треугольнике Паскаля? 16. Запишите формулу бинома Ньютона. 17. Сколько всего подмножеств имеет множество А, состоящее из п элементов? Запишите в явном виде все подмножества некоторого множества А, состоящего из 5 элементов. 18. Кто из ученых занимался комбинаторикой? 19. Решите уравнения:
Примеры решения некоторых комбинаторных задач Задача. Сколько пятизначных чисел можно записать цифрами 0, 1, 2, 3, 4 без повторений? Решение.Первую цифру можно выбрать четырьмя способами (нуль в качестве первой цифры не используется); оставшиеся незанятыми четыре цифры можно затем расположить в любом порядке. Это определяет следующее количество рассматриваемых пятизначных чисел: 4•4•3•2•1=96(чисел). Этот результат может быть получен и другими способами. Существует 5! перестановок из пяти цифр 0, 1, 2, 3, 4. Те из них, которые начинаются цифрой 0 (а их будет очевидно 4!), нужно исключить из рассмотрения. В итоге получаем: 5! – 4!=120 – 24=96(чисел). Ответ: 96 чисел. Задача. Сколько существует пятизначных чисел, в записи которых используются лишь цифры 0, 1, 2, 3, 4? Решение.Первая цифра может быть выбрана четырьмя способами (объясните почему), а каждая из последующих цифр – пятью способами, независимо от того, как выбраны предыдущие цифры. Следовательно, по правилу произведения, всего рассматриваемых чисел будет 4•5•5•5•5=2500(чисел). Ответ: 2500 чисел. Задача. Сколько существует пятизначных чисел, записываемых цифрами 0, 1, 2, 3, 4 без повторений, в которых центральная цифра является четной (0, 2 или 4)? Решение.Цифру 0 в качестве центральной цифры имеют 4! рассматриваемых числа: по числу способов, которыми можно заполнить первое, второе, четвертое и пятое места цифрами 1, 2, 3, 4. Цифру 2 на третьем месте имеют 3∙3! рассматриваемых чисел: первое место может быть занято тремя способами (1, 2, 3), а оставшиеся три места – второе, четвертое и пятое – распределяются между оставшимися тремя цифрами. Цифру 4 – так же, как и цифру 2 – имеют 3 • 3! рассматриваемых чисел. Далее, поскольку нас интересует хотя бы один из указанных трех случаев, используем комбинаторный принцип сложения. Всего рассматриваемых чисел существует: 4!+ 3• 3! +3• 3!=60(чисел). Ответ: 60 чисел. Задача. Сколько существует трехзначных чисел без повторяющихся цифр? Решение.Из 10 имеющихся цифр 0, 1, 2, ..., 9 можно составить следующее число размещений по 3: А Из них нужно исключить те размещения, которые начинаются цифрой 0; их будет очевидно A Следовательно, искомых трехзначных чисел будет А Ответ: 648 чисел. Задача. Семь девушек водят хоровод. Сколькими способами они могут стать в круг? Решение.Взаимное расположение любых семи точек В, С, D, Е, F, G на окружности однозначно определяется расположением по часовой стрелке шести точек В, С, D, Е, F, G относительно точки А. А таких расположений будет 6!=6 • 5 • 4 • 3 • 2 • 1=720. Таким образом, семь девушек могут стать в круг 720 способами. Ответ: 720 способов. Задача. Сколько ожерелий можно составить из 7 различных бусинок? Решение.Ожерелье можно перевернуть. Поэтому из семи различных бусинок можно составить 6! : 2=720 : 2=360(ожерелий). Ответ: 360 ожерелий. Задача. В лотерейном барабане m белых и n черных шаров, причем все они каким-то образом пронумерованы от 1 до (m+n). Сколькими способами из лотерейного барабана можно извлечь (a+s) шаров так, чтобы a из них были белыми, a s шаров были черными; а≤m, s≤n? Решение. Выбор нужных нам шаров из имеющихся (m+n) шаров осуществляется в два этапа. На первом этапе выберем а белых шаров (это можно сделать, очевидно, С Ответ: С Задача. Сколькими способами из колоды карт (36 листов) можно выбрать 4 карты так, чтобы среди них было 2 «дамы», причем одна – «дама пик»? Решение. Всю колоду карт разобьем на три части: к первой части отнесем даму пик, ко второй части – «дамы бубей», «червей» и «треф», к третьей части – остальные 32 карты. Задача состоит теперь в том, чтобы из первой части выбрать одну карту (это можно сделать единственным способом), из второй части выбрать также одну карту (это можно сделать тремя способами), из третьей части выбрать 2 карты (это можно сделать С Ответ: 1488 способами. До сих пор мы рассматривали задачи, в которых на порядок элементов в комбинациях не накладывалось никаких дополнительных условий. Либо допускался любой порядок элементов, либо порядок совсем не учитывался. Сейчас мы разберем несколько задач, в которых на порядок элементов налагаются некоторые ограничения[16]. Задача. Укротитель хищных зверей хочет вывести на арену цирка 5 львов и 4 тигров; при этом нельзя, чтобы два тигра шли друг за другом. Сколькими способами он может расположить зверей? Решение.Поставим сначала всех львов так, чтобы между каждыми двумя львами был промежуток. Это можно сделать 5!=120 способами. Число промежутков равно 4. Если присоединить к ним еще два места − впереди всех львов и позади них, то получится 6 мест, на которые можно поставить по тигру, тогда никакие два тигра не окажутся рядом друг с другом. Так как порядок тигров существен, то число способов их расстановки равно числу размещений из 6 по 4, то есть Ответ: 43200 способов. Если бы у дрессировщика было п львов и k тигров, то он мог бы решить задачу Задача. Сколькими способами можно переставить буквы слова «перемет» так, чтобы три буквы «е» не шли подряд? Решение. Сначала подсчитаем, во скольких перестановках все три буквы «е» идут подряд. Мы можем в этих перестановках объединить буквы «е» в один блок и переставлять этот блок вместе с буквами «п», «р», «м», «т». Получатся перестановок из 5 объектов, число которых равно Р=5!=120. А перестановок с повторениями из букв слова «перемет» можно составит Р(3, 1, 1, 1, 1)=840. Значит, число перестановок, в которых три буквы «е» не идут подряд, равно 840−120=720. Ответ: 720 способов. В этой задаче надо было найти число перестановок, подчиненных некоторому ограничительному условию − запрету трем буквам «е» стоять рядом. Такие задачи с различного вида ограничениями часто встречаются в комбинаторике. В некоторых из них можно применить тот же метод, что и в данной задаче: то есть объединить нескольких элементов в блоки. Задача. Четыре танкиста, четыре летчика и два артиллериста хотят сфотографироваться, стоя в один ряд, но так, чтобы представители одного рода войск стояли рядом. Сколькими способами они могут это сделать? Решение.Объединим танкистов, летчиков и артиллеристов в блоки, которые обозначим соответственно Т, Л, А. Из этих блоков можно сделать 3!=6 перестановок. Но еще можно переставлять фотографирующихся внутри блоков. Танкистов можно переставлять 4! способами, летчиков − тоже 4! способами, а артиллеристов − 2! способами. Всего по правилу произведения получаем 3!∙4!∙4!∙2!=6912 (способов). Ответ: 6912 способов. Вообще, пусть имеется Задача. Из плит сечением 30×50 см строится лестница, ведущая из точки А в точку В (см. рисунок 7). Расстояние АС равно 4,5м, а расстояние СВ − 1,5м. Высота каждой ступеньки равна 30 см, а ее ширина − целое кратное 50см. Сколькими способами можно построить лестницу?
Решение.Из условия задачи видно, что лестница должна иметь 5 ступенек и состоять из 9 «блоков» длиной 50см. Поэтому ступеньки можно строить в 10 местах − начиная с начала самой первой плиты (точки А) и кончая концом последней плиты (под точкой В). Таким образом, надо из 10 мест выбрать 5, а это можно сделать Ответ: 252 способов. Решенная задача похожа на задачу об укротителе: укротитель не хотел ставить рядом двух тигров, а строитель лестницы не может делать ступеньки двойной высоты. Но между этими задачами есть существенное отличие. Укротителю был важен порядок, в котором шли тигры. А для строителя лестницы все места, где есть подъем, одинаковы. Кроме того, укротитель должен был учитывать и порядок расположения львов, а для строителя лестницы все места, где можно сделать подъем, одинаковы. Поэтому выбор у строителя лестницы меньше, чем у укротителя. Если бы лестница имела высота 1,2 м и длину 2,5 м, то было бы 4 ступеньки и 6 мест, где их можно сделать. И ответ был бы В общем виде решенная задача формулируется так. Задача. Сколькими способами можно расставить m нулей и n единиц так, чтобы никакие две единицы не стояли рядом? Решение.В самом деле, каждую лестницу можно зашифровать последовательностью нулей и единиц: нуль означает место, где ломаная идет вправо, а единица − место, где она идет вверх. Например, лестница, изображенная на рисунке 14, шифруется так: 10010100010010. При этом, поскольку ступенек двойной высоты на лестнице не должно быть, в последовательности не могут идти две единицы подряд. Эта задача решается точно так же, как разобранный выше частный случай. Сначала выписываем т нулей. Для единиц получается (т+1) место − два места по краям и еще (m−1) мест в промежутках между нулями. На любое из этих (т+1) мест можно поставить одну из п единиц. Это может быть сделано Ответ: существует Задача. На книжной полке стоят двенадцать книг. Сколькими способами можно выбрать из них пять книг так, чтобы никакие две из них не стояли рядом? Решение.Эта задача сводится к только что решенной. Зашифруем каждый выбор книг последовательностью нулей и единиц: каждой оставленной книге сопоставим 0, а каждой взятой − 1. В результате получится последовательность из 5 единиц и 7 нулей. При этом, так как нельзя брать стоящие рядом книги, то в полученной последовательности не должно быть двух идущих подряд единиц. Но число последовательностей из 5 единиц и 7 нулей, в которых никакие две единицы не стоят рядом, равно Вообще, если на полке стоит п книг и выбираются k так, чтобы никакие две из них не стояли рядом, то это может быть осуществлено Общее число способов выбрать несколько книг из п так, чтобы выбираемые книги не стояли рядом, равно Задача. За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями (и только с ними). Надо выбрать 5 рыцарей, чтобы освободить заколдованную принцессу, но среди выбранных рыцарей не должно быть врагов. Сколькими способами это можно сделать? Решение.Эта задача похожа на задачу о книжной полке, но отличается от нее тем, что рыцари сидят не в ряд, а по кругу. Но ее легко свести к случаю, когда рыцари сидят в ряд. Для этого возьмем какого-нибудь рыцаря, скажем, сэра Ланселота. Все выбираемые комбинации рыцарей распадаются на два класса − в одних из них сэр Ланселот участвует, а в других нет. Подсчитаем, сколько комбинаций входит в каждый класс Если сэр Ланселот отправляется освобождать заколдованную принцессу, то ни его сосед справа, ни его сосед слева уже не примут участия в этой экспедиции. Остаются 9 рыцарей, из которых надо выбрать 4 спутников для сэра Ланселота. Так как соседи Ланселота не участвуют в экспедиции, то надо лишь проследить, чтобы среди выбранных 4 рыцарей не было врагов, то есть чтобы никакие два из них не сидели рядом. Но исключение сэра Ланселота и его двух соседей разрывает цепь рыцарей, и можно считать, что они сидят не за круглым столом, а в один ряд. А в этом случае выбрать 4 рыцарей из 9 требуемым образом можно Теперь подсчитаем, сколько комбинаций входит во второй класс. Так как сэр Ланселот не участвует в экспедиции, то его можно сразу исключить из числа рыцарей круглого стола. Тогда цепь рыцарей разрывается, и остаются 11 рыцарей расположенных в ряд. Из них надо выбрать 5 участников экспедиции так, чтобы среди выбранных не было двух сидящих рядом. Это можно сделать Ответ: 36 способов. Вообще, если за круглым столом сидят п рыцарей, и надо выбрать к рыцарей так, чтобы в их число не попали никакие два соседа, то это можно сделать Все комбинации рыцарей разбивают на два класса в зависимости от того, участвует или нет в них рыцарь Ланселот. Комбинаций, где он участвует, будет Легко проверяется, что Например, при п=12, k=5 получаем |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1513. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
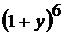 ; 2)
; 2) 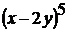 ; 3)
; 3) 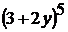 ; 4)
; 4) 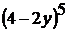 ;
; 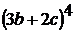 ; 6)
; 6) 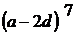 ; 7)
; 7) 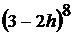 ; 8)
; 8) 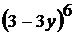
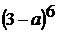 ;
;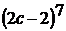 ;
;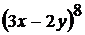 ;
;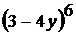 .
.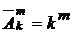 .
.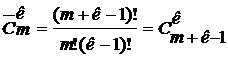 .
.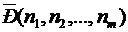
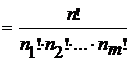 .
.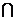 B)
B) 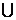 (B\A); (A
(B\A); (A 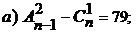 б)
б) 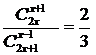 ; в)
; в) 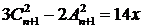 .
.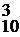 = 10 • 9 • 8 = 720.
= 10 • 9 • 8 = 720.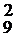 =9 • 8=72.
=9 • 8=72. – A
– A  =720 – 72=648(чисел).
=720 – 72=648(чисел).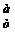 способами), а на втором этапе – s черных шаров (это можно сделать
способами), а на втором этапе – s черных шаров (это можно сделать 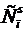 способами). По комбинаторному правилу произведения извлечь а белых и s черных шаров из рассматриваемого лотерейного барабана можно следующим числом способов: С
способами). По комбинаторному правилу произведения извлечь а белых и s черных шаров из рассматриваемого лотерейного барабана можно следующим числом способов: С 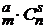 .
.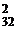 способами). По комбинаторному правилу произведения всего для рассматриваемого выбора четырех карт существует
способами). По комбинаторному правилу произведения всего для рассматриваемого выбора четырех карт существует 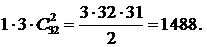
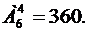 Комбинируя каждый способ расстановки львов с одним из способов расстановки тигров, получаем 120∙360=43200 (способов) вывести хищных зверей на арену.
Комбинируя каждый способ расстановки львов с одним из способов расстановки тигров, получаем 120∙360=43200 (способов) вывести хищных зверей на арену.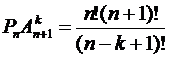 способами. Это возможно при условии, что k<n+1 − иначе 2 тигра окажутся рядом.
способами. Это возможно при условии, что k<n+1 − иначе 2 тигра окажутся рядом. предметов одного типа,
предметов одного типа,  предметов другого типа, ...,
предметов другого типа, ...,  предметов k-го типа, где предметы одного и того же типа все же различимы друг от друга. Тогда число перестановок этих предметов, в которых все предметы одного и того же типа стоят рядом, равно
предметов k-го типа, где предметы одного и того же типа все же различимы друг от друга. Тогда число перестановок этих предметов, в которых все предметы одного и того же типа стоят рядом, равно 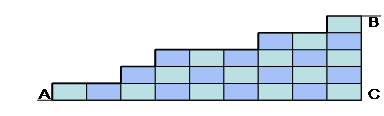 Рис.7
Рис.7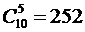 способами.
способами.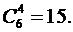 А у укротителя в точно таком же случае получилось 43200 вариантов.
А у укротителя в точно таком же случае получилось 43200 вариантов.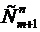 способами.
способами.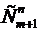 способов расставить т нулей и n единиц так, чтобы никакие две единицы не шли рядом.
способов расставить т нулей и n единиц так, чтобы никакие две единицы не шли рядом.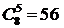 .
.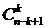 способами. Отсюда видно, что задача разрешима при
способами. Отсюда видно, что задача разрешима при 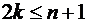 .
.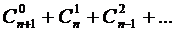
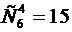 способами. Итак, в первый класс входит 15 комбинаций.
способами. Итак, в первый класс входит 15 комбинаций.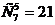 способами. Таким образом, общее число способов равно 15+21=36.
способами. Таким образом, общее число способов равно 15+21=36.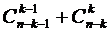 способами.
способами.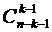 , а комбинаций, в которые он не входит,
, а комбинаций, в которые он не входит, 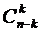 .
.