
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Правила суммы и произведенияРешение большинства комбинаторных задач основано на правилах, которые называют правилами суммы и произведения. Рассмотрим следующие задачи: Задача 1. В магазине «Магнит» имеется 20 плиток молочного шоколада с орехами «ALPEN GOLD» и 14 плиток черного пористого шоколада «ВОЗДУШНЫЙ». Сколькими способами можно выбрать одну плитку шоколада? Задача 2. В книжном магазине «Феникс» имеется 5 книг о Гарри Поттере и 3 книги из серии «Властелин колец». Сколькими способами можно выбрать одну книгу? Эти задачи переведём на язык теории множеств и сформулируем в общем виде: Имеются два конечных множества А={а В комбинаторике, которая возникла раньше теории множеств, правило нахождения числа элементов в объединении двух непересекающихся конечных множеств называют правилом суммы и формулируют в следующем виде. Если объект а можно выбрать m способами, а объект b можно выбрать k способами, отличными от способа выбора объекта a, то выбор «либо a, либо b» можно осуществить m+k способами. Правило суммы распространяется и на тот случай, когда число попарно непересекающихся множеств более двух. Мы можем решить ранее предложенные задачи, используя правило суммы. Задача 1. Решение. Так как имеется 20 видов молочного шоколада с орехами «ALPEN GOLD», то существует 20 способов выбрать одну из плиток шоколада. Аналогично существует 14 способов выбора одной плитки шоколада «ВОЗДУШНЫЙ». Так как требуется выбрать шоколад «либо с орехами, либо пористый», то по правилу суммы получаем (20+14=34) тридцать четыре способа выбора одной плитки шоколада.  Задача 2. Решение. Рассуждая также, как при решении задачи 1, по правилу суммы получим 8 способов выбора одной книги из предложенных. Рассмотрим следующие задачи. Задача 3. Ко Дню Именинника, отмечаемого в начальной школе, родители приготовили детям подарки: 9 книг художественной литературы различных писателей и 5 видов блокнотов. Сколькими способами можно выбрать подарок, состоящий из одной книги и одного блокнота? Задача 4. Сколькими способами можно составить команду из одного спортсмена по прыжкам в длину и одного бегуна, которые являются претендентами для участия в соревнованиях по легкой атлетике, если среди претендентов на участие 7 спортсменов по прыжкам в длину и 4 спортсмена по бегу? Переведём эти задачи на язык теории множеств и сформулируем в общем виде: Имеются два конечных множества А={а В теории множеств решение таких задач сводится к нахождению числа элементов в декартовом произведении множеств. В комбинаторике правило, по которому решаются подобные задачи, называют правилом произведения. Если объект а можно выбрать n способами, а объект b можно выбрать m способами, то выбор «и a, и b» можно осуществить n ∙ m способами. Правило произведения распространяется на случай выбора кортежа любой длины. Используя правило произведения, решим задачи, предложенные ранее. Задача 3. Решение. Так как существует 9 способов выбора книг по художественной литературе и 5 способов выбора блокнотов, то по правилу произведения «выбор книги и блокнота» («и a, и b») можно осуществить (9∙5=45) сорока пятью способами. Ответ: 45 способов. Задача 4. Решение. Рассуждая также как при решении задачи 4, по правилу произведения получим 28 способов составить команду для участия в соревнованиях по легкой атлетике. Ответ: 28 способов. Рассмотрим еще несколько задач. Задача 5. Определим, сколькими способами можно выбрать гласную и согласную буквы из слова «здание»? а из слова «микрон»? Решение.В слове «здание» 3 согласные и 3 гласные буквы. Нам необходимо выбрать и гласную и согласную буквы, поэтому по правилу произведения выбор может быть произведен 3∙3 = 9 (способами). А из слова «микрон» выбор можно сделать 4∙2=8 (способами). Ответ: 9 способами, 8 способами. Задача 6. В конкурсе принимают участие 20 человек. Сколькими способами можно присудить первую, вторую и третью премии? Решение.Существует 20 способов выбора одного кандидата на первую премию. Остается 19 кандидатов, одному из которых присуждают вторую премию. Наконец, одному из восемнадцати оставшихся кандидатов присуждают третью премию. Согласно правилу произведения для этого существует 20 • 19 • 18=6840 (способов) присуждения первой, второй и третьей премии. Ответ: 6840 способов. Задача 7. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9? Решение. Так как запись числа не может начинаться с нуля, то цифру разряда сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить шестью способами, выбрать цифру единиц из данных шести также можно шестью способами. Отсюда, по правилу произведения, получаем, что всего трехзначных чисел (из данных шести цифр) можно образовать 5•6•6=300(чисел). Ответ: 300 чисел. Задача 8. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 3, 6, 7 и 9, если каждая из них может быть использована в записи числа только один раз? Решение. Так как запись числа не может начинаться с нуля, то цифру разряда сотен можно выбрать пятью способами; выбор цифры десятков можно осуществить также пятью способами, поскольку цифры в записи числа не должны повторяться, а одна из шести данных цифр будет уже использована для записи сотен; После выбора двух цифр (для записи сотен и десятков) выбрать цифру единиц из данных шести можно четырьмя способами. Отсюда, по правилу произведения, получаем, что всего трехзначных чисел (из данных шести цифр) можно образовать 100: 5•5•4=100(чисел). Ответ: 100 чисел. Докажем теорему 5, используя правило произведения. Теорема 5. Конечное множество, содержащее п элементов, имеет 2п подмножеств, то есть если Ап = {а1, а2, ... , a Перенумеруем элементы множества А и для каждого подмножества множества А построим последовательность длины n из нулей и единиц по следующему правилу: на k – м месте пишем 1, если элемент с номером k входит в подмножество, и 0, если элемент с номером k не входит в подмножество. Итак, каждому подмножеству соответствует своя последовательность нулей и единиц. Число всех возможных последовательностей длины n, составленных из нулей и единиц, равно, согласно правилу произведения: 2 ∙ 2 ∙ … ∙ 2=2 Следовательно, и число всех подмножеств множества А равно 2 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1307. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , а
, а  , … , а
, … , а  } и В={b
} и В={b  , b
, b 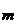 }, не имеющих общих элементов. Сколькими способами можно выбрать объект, принадлежащий или А, или В?
}, не имеющих общих элементов. Сколькими способами можно выбрать объект, принадлежащий или А, или В?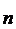 } и В={b
} и В={b 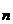 }, то п(М(Ап))=2п.
}, то п(М(Ап))=2п.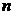 .
. . Теорема доказана.
. Теорема доказана.