
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перестановки с повторениямиОпределение. Перестановкой с повторениями из m элементов состава k1, k2,…,km называют кортеж длины суммы k1+k2+…+km, где k1 – число повторений одного элемента множества, k2 – число повторений другого элемента множества и т.д., km – количество повторений оставшегося элемента множества. Обозначают: Теорема 10.Число различных перестановок с повторениями данного состава (n1, n Рассмотрим одну перестановку и заменим в ней все одинаковые элементы разными. Тогда число различных перестановок, которые можно составить из рассматриваемой нами перестановки, по правилу произведения равно n1, n Следовательно, Теорема доказана. Задача. Сколькими способами можно расставить белые фигуры: 2 коня, 2 слона, 2 ладьи, ферзя и короля на первой линии шахматной доски? Решение.В этой задаче надо найти число кортежей длины 8, имеющих заданный состав (2, 2, 2, 1, 1). Число таких кортежей, то есть перестановок с повторениями, равно 5040.
Ответ: 5 040 способами. Общую задачу о перестановках с повторениями можно сформулировать следующим образом: имеются предметы m различных типов. Сколько перестановок можно сделать, взяв n1 элементов первого типа, n2 типа, ..., nm элементов m-го типа? Задача. Сколько различных буквенных комбинаций (не обязательно имеющих смысл) можно получить, переставляя буквы слова «кишмиш»? Решение.В данном слове одна буква «к», две буквы «и», две буквы «ш», одна буква «м», всего 1+2+2+1=6 (букв). Значит, Р(1,2,2,1)= Ответ: 180 слов. Задачи для самостоятельного решения  1. Сколько слов, состоящих из восьми букв, можно образовать из 6 букв алфавита? 2. В магазине имеется 7 видов тетрадей в клеточку. Сколькими способами можно купить 12 тетрадей? 3. Сколькими способами можно расставить белые фигуры: два коня, две ладьи, ферзя и четыре пешки – на одной линии шахматной доски? 4. Сколько будет костей геометрического домино, если использовать в их образовании следующие геометрические фигуры: квадрат, треугольник, круг, ромб? 5. Сколько различных буквенных комбинаций (не обязательно имеющих смысл) можно получить, переставляя буквы слова «комбинаторика»? Переставляя буквы слова «математика»? 6. Сколькими способами можно обить 12 стульев, если имеется 5 сортов обивочного материала? Бином Ньютона В алгебре довольно часто приходится возводить в степень двучлен (a+b). Недаром каждый школьник заучивает наизусть формулы квадрата и куба суммы двух чисел. Аналогичная формула, но уже для произвольного натурального числа п≥1 называютбиномом Ньютона, хотя и была известна задолго до того времени, когда жил Ньютон. Слово «бином» в переводе с латыни означает «двучлен». Теорема 11.Для любого целого неотрицательного n справедливо тождество:
Левая часть равенства является произведением n одинаковых сомножителей:
Каждое слагаемое в этой сумме имеет вид слова в алфавите {x,y}, в котором i–тую позицию занимает переменная, выбираемая из i–того сомножителя. Нетрудно видеть, что каждое слово длины n появится в этом выражении в точности один раз. После группировки сомножителей каждое слово, в котором буква x встречается k раз, превращается в слагаемое вида Ранее были приведены следующие свойства биномиальных коэффициентов: 1) 2) 3) Особенно важным свойством является последнее. Оно позволяет с помощью одних только операций сложения найти все числа сочетаний из n элементов, если известны числа сочетаний из ( Треугольник Паскаля является, пожалуй, одной из наиболее известных и изящных числовых схем во всей математике. Блез Паскаль, французский математик и философ, посвятил ей специальный «Трактат об арифметическом треугольнике». Впрочем, эта треугольная таблица была известна задолго до 1665 года – даты выхода в свет трактата. Так, в 1529 году треугольник Паскаля был воспроизведен на титульном листе учебника арифметики, написанного астрономом Петром Апианом.
Изображен треугольник и на иллюстрации книги «Яшмовое зеркало четырех элементов» китайского математика Чжу Шицзе, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника в 1110 году, в свою очередь, заимствовав его из более ранних китайских или индийских источников. В треугольнике Паскаля биномиальные коэффициенты располагаются следующим образом: C . . . . . . . . . В этой бесконечной таблице строка с номером n (n=0,1,2,...) образована числами C В треугольнике Паскаля прослеживаются следующие закономерности. 1. Члены всякой строки треугольника Паскаля сначала возрастают (до середины строки), а затем − убывают. Например, 1<4<6, 6>4>1 (четвертая строка); 1<5<10, 10>5>1 (пятая строка). 2. Всякая строка треугольника Паскаля симметрична относительно своей середины (то есть члены всякой строки треугольника Паскаля, равноудаленные от ее краев, равны между собой). Формально это свойство записывается в виде упоминавшегося нами равенства 3. Сумма членов n-й строки треугольника Паскаля равна 2 То есть 4. Всякое непустое множество имеет столько подмножеств с четным числом элементов, сколько и подмножеств с нечетным числом элементов; иными словами, при n≤1 C Данное соотношение получается применением формулы бинома Ньютона к левой части тождества (1 – 1)п=0. С помощью утверждения 3 можно конкретизировать: C Приведем комбинаторное доказательство этого утверждения. С каждым подмножеством X данного непустого множества А={а1, а2, ... , ап} свяжем подмножество Y, определяемое следующим образом: Y получается из X путем исключения или, наоборот, путем добавления к нему элемента аi в зависимости от того, содержит X элемент аi или не содержит. Все подмножества множества А можно таким образом разбить на пары подмножеств (X, У), причем в каждой такой паре одно из подмножеств содержит четное, а другое – нечетное число элементов. Следовательно, подмножеств с четным числом элементов столько же, сколько и подмножеств с нечетным числом элементов. 5. Крайние члены треугольника Паскаля равны 1. Каждый же из остальных членов равен сумме двух смежных с ним членов, стоящих в предыдущей строке. Например (см. строку с номером п=4), 4=1 + 3; 6=3 + 3; 4=3 + 1. В общем случае (при 1≤m≤п) C Последняя формула интересна и тем, что несет в себе правило построения каждой последующей строки треугольника Паскаля по предыдущей строке. Доказать это равенство можно непосредственными вычислениями с помощью формулы Однако гораздо интересней обратиться к ее комбинаторной трактовке: тех сочетаний из элементов { а1, а2, ... , ап, an+1} по т, которые не содержат ап+1, будет, очевидно, С 6. Это получается при 7. Получается применением формул Рассмотрим примеры использования формулы бинома. Пример. Разложить по формуле бинома Ньютона двучлен Решение. Пример. Разложить по формуле бинома Ньютона двучлен Решение. Пример. Запишите формулу Бинома Ньютона для (х–2у)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
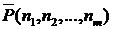 .
.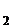 , ..., n
, ..., n 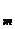 ) вычисляют по формуле
) вычисляют по формуле 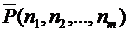
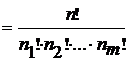 , где n =n1 +n
, где n =n1 +n 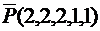
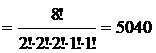 .
.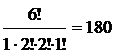 (слов).
(слов).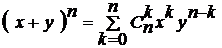 .
.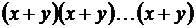 . Если раскрыть скобки, не приводя подобных и не группируя одинаковые сомножители в степени, получится сумма, в которой каждое слагаемое является произведением n переменных, по одной из каждого сомножителя. Например,
. Если раскрыть скобки, не приводя подобных и не группируя одинаковые сомножители в степени, получится сумма, в которой каждое слагаемое является произведением n переменных, по одной из каждого сомножителя. Например,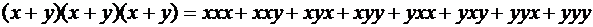 .
.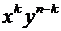 . Таких слов имеется ровно C
. Таких слов имеется ровно C 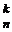 , поэтому после приведения подобных получается правая часть равенства.
, поэтому после приведения подобных получается правая часть равенства.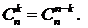 ; 4)
; 4) 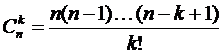 ;
;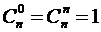 ; 5)
; 5) 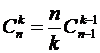 ;
;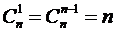 ; 6)
; 6) 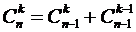 .
.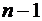 ) элемента. Это же свойство лежит в основе построения таблицы биномиальных коэффициентов, называемой треугольником Паскаля.
) элемента. Это же свойство лежит в основе построения таблицы биномиальных коэффициентов, называемой треугольником Паскаля.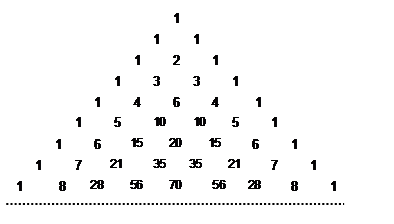
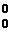
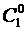
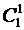
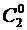
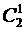
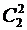
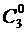
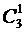
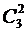
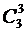
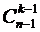 и
и 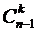 , сумма которых, по свойству 6), как раз и равна C
, сумма которых, по свойству 6), как раз и равна C 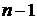 ) заполнена, то легко заполняется строка с номером n: первый и последний элементы всегда равны 1, а каждый из остальных получается сложением двух расположенных над ним элементов предыдущей строки.
) заполнена, то легко заполняется строка с номером n: первый и последний элементы всегда равны 1, а каждый из остальных получается сложением двух расположенных над ним элементов предыдущей строки.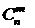
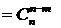 .
.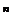 .
.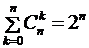 . Это можно рассматривать как следствие формулы бинома Ньютона, если положить
. Это можно рассматривать как следствие формулы бинома Ньютона, если положить 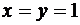 . Важно, однако, разобраться в теоретико-множественной интерпретации данного свойства. Число
. Важно, однако, разобраться в теоретико-множественной интерпретации данного свойства. Число 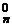 + C
+ C 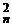 + C
+ C 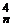 + …=C
+ …=C  + C
+ C 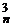 + C
+ C 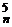 + …
+ …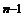 .
.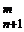 =C
=C 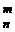 + C
+ C 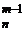 .
.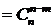 .
.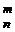 ; тех же сочетаний, которые содержат an+1, будет C
; тех же сочетаний, которые содержат an+1, будет C 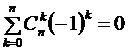 .
.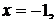
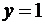 .
.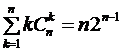 .
.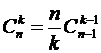 и
и 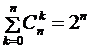 .
.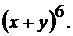
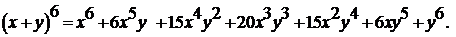
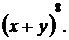
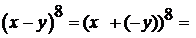
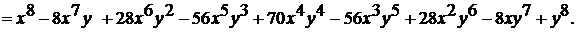
 .
.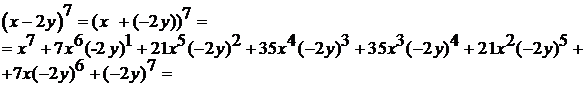 =
= 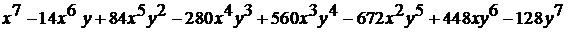 .
.