
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Частные производные функции двух переменных
Переменная z называется функцией двух независимых переменных х и у на некотором множестве точек Пишут:
С геометрической точки зрения функция Если при Таким образом, по определению
Аналогично,
Так как
Пример 1 Найти частные производные функции Решение
Пример 2 Показать, что функция Решение Найдем частные производные
Подставим найденные выражения в левую часть уравнения:
Дифференциал функции двух переменных
Частным дифференциалом функции выражение выражение 
Пример 1 Найти частные дифференциалы функции Решение
Полный дифференциал функции
Пример 2 Найти дифференциал Решение Найдем частные производные
Подставим частные производные в формулу полного дифференциала, получим
Краткое содержание (программа) курса
Элементы линейной алгебры Матрицы, операции над ними. Определители и их свойства и вычисление. Ранг матрицы, обратная матрица. Теорема Кронекера-Капелли. Решение систем линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса.Система m линейных уравнений с n неизвестными.
Элементы векторной алгебры и аналитической геометрии Линейные операции над векторами. Декартова прямоугольная система координат. Координаты вектора. Направляющие косинусы и длина вектора. Скалярные и векторные величины. Скалярное, векторное и смешанное произведение векторов. Прямая на плоскости. Расстояние от точки до прямой. Угол между прямыми. Геометрический смысл линейных неравенств и их систем. Кривые второго порядка: эллипс, гипербола, парабола, их канонические уравнения. Аналитическая геометрияв пространстве. Уравнение плоскости в пространстве. Прямая в пространстве. Основные задачи на прямую и плоскость в пространстве. Преобразование координат. Полярная система координат.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 786. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , если каждой паре значений
, если каждой паре значений  из множества
из множества  соответствует определенное значение величины z.
соответствует определенное значение величины z. .
. представляет собой поверхность.
представляет собой поверхность. отношение частного приращения функции к вызвавшему его приращению аргумента
отношение частного приращения функции к вызвавшему его приращению аргумента  имеет конечный предел, то этот предел называется частной производной функции
имеет конечный предел, то этот предел называется частной производной функции  по независимой переменной х в точке
по независимой переменной х в точке 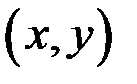 и обозначается
и обозначается  , или
, или  , или
, или  .
. .
. .
. вычисляется при неизменном значении переменной у, а
вычисляется при неизменном значении переменной у, а  – при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции
– при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции  называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции
называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции  называется ее производная по у, вычисленная в предположении, что х – постоянная.
называется ее производная по у, вычисленная в предположении, что х – постоянная. .
.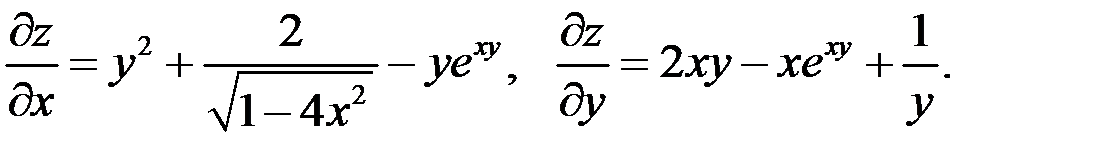
 удовлетворяет уравнению
удовлетворяет уравнению  .
. ,
, .
.
 что и требовалось доказать.
что и требовалось доказать. называется произведение частной производной на соответствующее произвольное приращение независимой переменной:
называется произведение частной производной на соответствующее произвольное приращение независимой переменной: называется частным дифференциалом функции
называется частным дифференциалом функции  по переменной х;
по переменной х; называется частным дифференциалом функции
называется частным дифференциалом функции  по переменной у.
по переменной у.
 ,
,  .
. равен сумме ее частных дифференциалов:
равен сумме ее частных дифференциалов: .
. функции
функции  .
. ,
, .
.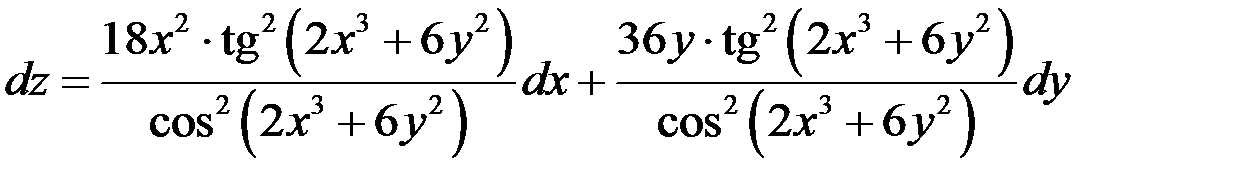 .
.