
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная сложной функции
Пусть дана сложная функция Теорема. Если функция
Замечание. Теорема может быть обобщена на случай любой конечной цепочки функций. Так, если Пример Найти производную функции Решение Здесь
Исследование функций и построение графиков функций Одна из возможных схем исследования функции и построения ее графика включает следующие этапы решения задачи:
1. Найти область определения функции. 2. Найти точки пересечения графика функции с осями координат. 3. Определить четность, нечетность. 4. Найти точки разрыва функции и асимптоты графика функции. 5. Исследовать функцию на экстремум, найти интервалы монотонности функции, точки максимума и минимума. 6. Найти интервалы выпуклости, вогнутости графика функции и точки перегиба. 7. Построить график функции.
Пример С помощью методов дифференциального исчисления исследовать и построить график функции Решение 1. Область определения функции находится из условия: 2. Точки пересечения графика функции с осями координат: с осью Оу, с осью Ох, 3. Четность, нечетность. Функция В нашем случае,  4. Точки разрыва функции и асимптоты графика функции. 1) Вертикальные асимптоты. Прямая
равен Заданная функция имеет две точки разрыва второго рода
следовательно, график функции имеет две вертикальных асимптоты 2) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
Если эти пределы конечны и различны, то прямые Так как
то график функции имеет горизонтальную асимптоту
3) Наклонные асимптоты. Пусть прямая
Аналогично находится асимптота при Так как
5. Исследование функции на экстремум. Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель
_ _ _ х -6 6 у
6. Исследование на выпуклость, вогнутость. Точки перегиба. Вычислим производную второго порядка:
_ + _ + х Так как при переходе через точку
7. Построение графика функции.
Тема № 4
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 576. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 где
где  или
или  .
. дифференцируема в точке
дифференцируема в точке  , а функция
, а функция  дифференцируема в точке
дифференцируема в точке  , тогда сложная функция
, тогда сложная функция  дифференцируема в точке
дифференцируема в точке  , причем
, причем или
или 
 , или
, или  и существуют производные
и существуют производные  , то
, то  .
. .
. ,
, , тогда
, тогда  .
. .
. , т.е.
, т.е.  .
. , точка
, точка  ,
, , точка
, точка  .
. называется четной, если для любого х из области определения справедливо равенство
называется четной, если для любого х из области определения справедливо равенство  . Функция
. Функция  . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
. Если не выполнено ни одно из равенств, то функцию называют функцией общего вида. , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
, следовательно, функция нечетная, а ее график симметричен относительно начала координат. является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  , если хотя бы один из пределов
, если хотя бы один из пределов или
или 
 или
или  . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
. Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот. и
и  , так как
, так как ,
, 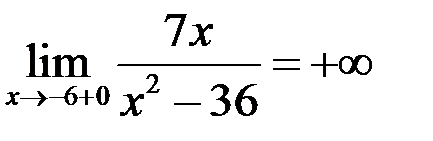 ,
, ,
, 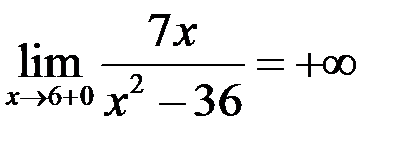 ,
, и
и  .
.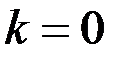 .
. .
. будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен
будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен  , то не существуют и соответствующие асимптоты.
, то не существуют и соответствующие асимптоты. ,
, .
. является асимптотой графика функции
является асимптотой графика функции  . Такую асимптоту называют наклонной. Для того, чтобы график функции
. Такую асимптоту называют наклонной. Для того, чтобы график функции  имел при
имел при  наклонную асимптоту
наклонную асимптоту  , необходимо и достаточно, чтобы существовали оба предела:
, необходимо и достаточно, чтобы существовали оба предела: .
. .
. , то наклонных асимптот нет.
, то наклонных асимптот нет. .
. к нулю:
к нулю: , т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
 Необходимое условие точки перегиба:
Необходимое условие точки перегиба:  или не существует. Равенство
или не существует. Равенство  выполняется при
выполняется при  , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
, следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
 -6
-6  0
0  6
6  у
у вторая производная меняет знак, то точка с абсциссой
вторая производная меняет знак, то точка с абсциссой  .
.