
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вычисление пределов с использованием второго замечательного предела
Одна из форм записи второго замечательного предела
Второй замечательный предел раскрывает неопределенность вида
Пример Вычислить предел Решение Предел основания
и применим второй замечательный предел:
Непрерывность функции
Пусть функция Определение. Функция
Таким образом, для того чтобы функция 1) функция 2) должны существовать пределы функции 3) эти пределы должны быть равны между собой и равны значению функции Если хотя бы одно из этих условий не выполнено, то говорят, что функция имеет разрыв в точке Точки разрыва следует искать среди точек, не входящих в область определения функции. Классификация точек разрыва
Определение. Если в точке
или функция не определена, то точка В этом случае функцию можно доопределить в точке
Определение. Если в точке  При переходе через точку
Определение. Точка
Пример В точках Решение Область определения функции Исследуем точку если если
Так как односторонние пределы конечны, но не равны между собой, то в точке Исследуем точку если если Так как односторонние пределы равны
Правила дифференцирования
Определение. Производной функции
По определению
Таблица производных
Правила дифференцирования
1. Производная постоянной равна нулю: 2. Теорема. Если каждая из функций 1) 2) 3) Следствие. Постоянный множитель можно выносить за знак производной:
Пример Используя таблицу производных и правила дифференцирования, найти производную функции Решение
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 545. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
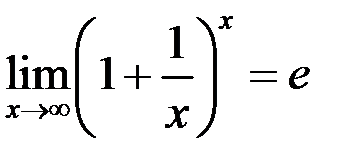 .
. .
. .
. , а показатель степени
, а показатель степени  при
при 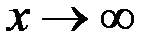 , т.е. имеет место неопределенность вида
, т.е. имеет место неопределенность вида  . Выделим целую часть основания степени
. Выделим целую часть основания степени

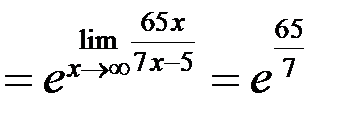 , учитывая, что
, учитывая, что  .
. определена в некоторой окрестности точки
определена в некоторой окрестности точки 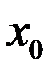 .
. называется непрерывной в точке
называется непрерывной в точке  , если она имеет предел в точке
, если она имеет предел в точке  и этот предел равен
и этот предел равен  – значению функции
– значению функции  в точке
в точке 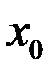 :
: .
.  была непрерывна в точке
была непрерывна в точке  , необходимо и достаточно выполнение трех условий:
, необходимо и достаточно выполнение трех условий: должна быть определена в точке
должна быть определена в точке  ;
; при
при  как слева, так и справа, т.е.
как слева, так и справа, т.е.  и
и  ;
; в точке
в точке  , т.е.
, т.е.  .
. и точку
и точку 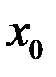 называют точкой разрыва функции
называют точкой разрыва функции 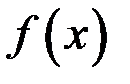 .
. функция
функция  имеет пределы слева и справа и они равны между собой, а в точке
имеет пределы слева и справа и они равны между собой, а в точке 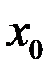
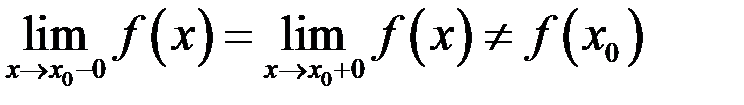
 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции  .
.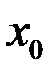 так, чтобы она стала непрерывной, т.е. положить
так, чтобы она стала непрерывной, т.е. положить .
. функция
функция  имеет конечные пределы слева и справа, причем
имеет конечные пределы слева и справа, причем  , то точка
, то точка  называется точкой разрывафункции
называется точкой разрывафункции 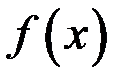 1-го рода.
1-го рода. значение функции
значение функции  претерпевает скачок, измеряемый разностью
претерпевает скачок, измеряемый разностью  .
.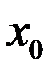 называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен
называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен  .
. и
и  для функции
для функции 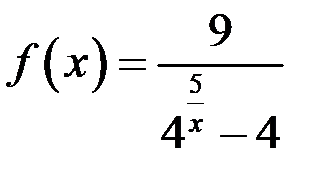 установить характер точек разрыва.
установить характер точек разрыва.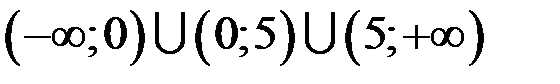 . Данная функция непрерывна во всех точках, кроме точек
. Данная функция непрерывна во всех точках, кроме точек 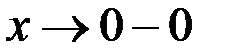 , то
, то  , тогда предел слева
, тогда предел слева  ,
, , то
, то 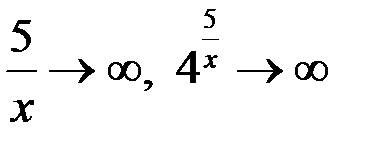 , тогда предел справа
, тогда предел справа  .
. имеет разрыв 1-го рода (скачок функции).
имеет разрыв 1-го рода (скачок функции). , находя ее односторонние пределы в этой точке:
, находя ее односторонние пределы в этой точке: , то
, то  , тогда
, тогда 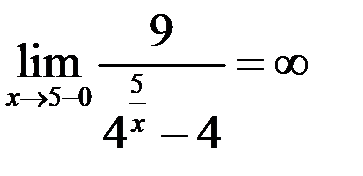 ,
,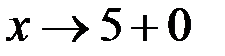 , то
, то  , тогда
, тогда  .
.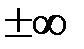 , то в точке
, то в точке  имеет разрыв 2-го рода.
имеет разрыв 2-го рода. в данной точке х называется предел отношения приращения функции к приращению аргумента, при
в данной точке х называется предел отношения приращения функции к приращению аргумента, при  , если он существует.
, если он существует. .
. ,
, 





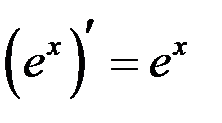







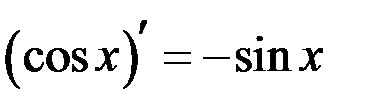



 .
. и
и  дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии
дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии  ) так же дифференцируемы в этой точке, причем имеют место формулы:
) так же дифференцируемы в этой точке, причем имеют место формулы: ,
, ,
, .
. .
.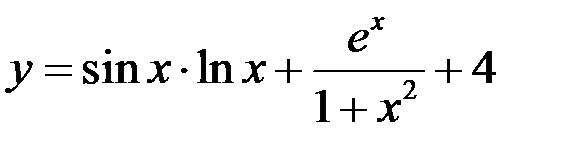 .
.