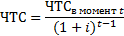Применение методов математического программирования для выбора оптимального набора проектов и последовательности их реализации

В случае отсутствия ограничений на ресурсы, которые доступны предприятию, для принятия положительного решения об эффективности проекта, который входит в группу взаимно независимых проектов, необходимо, чтобы ЧТС для данного проекта был положительным.

При выборе варианта среди взаимоисключающих про­ектов, которые имеют положительные ЧТС, необходимо при­нять тот проект, у которого ЧТС имеет максимальное значе­ние.

При наличии ограничений на ресурсы (финансовых, про­изводственных мощностей, трудовых и т. д.), которые доступ­ны предприятию, задача выбора набора проектов, которые приносят наибольший доход, может быть решена методами математического программирования и в самой общей поста­новке может быть сведена к задаче целочисленного програм­мирования [1]. Когда денежные потоки проектов и другие параметры проектов не меняются в зависимости от принятия или отказа от проектов из рассматриваемого набора, задача может быть сведена к задаче целочисленного линейного про­граммирования. Этот случай является практически наиболее важным. Формулировка задачи выбора оптимального набора проекта в линейном случае выглядит следующим образом [39]. Необходимо найти максимум функции L,который имеет смысл ЧТС от реализации предприятием оптимального набо­ра проектов:

L= ∑xiNPVi

при условии соблюдения ограничений

∑xiK¹it≤¹t,.. .,∑xiK^dit≤K^dit, i=l i=1

Xiϵ{0,1},

t= 1..... T

i= 1..... n

где NPVi- ЧТС i-го проекта,n-число проектов, К^mit - потребность в m-ом ресурсе в период tдля i-гoпроекта, К^mt- ограничение на m-ый ресурс в момент t, Т — горизонт плани­рования, xi- переменная, равная 0 или 1, xi=0 соответствует отказу от проекта, а х_i= 1 соответствует принятию проекта,d- число ресурсов.

Кроме того, могут добавляться ограничения, которые вы­ражают зависимость между проектами. Например, если про­екты iи jявляются взаимоисключающими, то необходимо добавить ограничение

Xi+Xj≤ 1.

Если проекты iи jявляются взаимообусловленными, то должно выполняться ограничение

Xi- Xj=0.

Часто возникает задача о выборе оптимальной по­следовательности реализации набора проектов. В этом случае реализация проекта в разные моменты времени рассматри­вается как набор взаимоисключающих проектов. При этом ЧТС проекта, который начинает реализовываться в момент времени tпутем дисконтирования, приводится к начальному моменту времени, т. е.

где i- норма дисконта.

При решении задачи целочисленного линейного программирования используются специальные методы, которые широко известны и описаны в литературе.

Необходимо отметить, что подходу на основе метод_0в математического программирования присущи некоторыепринципиальные ограничения, которые связаны с тем, что принимается допущение об известности всех будущих ин­вестиционных альтернатив. В действительности процессформирования инвестиционных предложений является не­прерывным. Кроме того, ограничения могут быть достаточно точно известны только для начальных периодов. Поэтому результаты должны постоянно пересматриваться по мере по­ступления новой информации.

При большом числе проектов n, процесс решения задач целочисленного линейного программирования является тру­доемким, требует больших затрат времени и использования специальных программных средств.

Несмотря на эти естественные и в большинстве случаев неустранимые трудности методы математического програм­мирования предоставляют систематический и применимый на практике инструмент для решения задачи выбора оптималь­ного набора проектов.

Однако при относительно небольшом числе проектов ре­шение может быть получено сравнительно просто путем пе­ребора всевозможных комбинаций значений переменных Xj, j=l,...,n,которые должны удовлетворять всем ограничениям и принимать значения 0 или 1. Например, в случае n=3 необхо­димо рассчитать значение функционала Lдля 8 вариантов значений переменных x₁,x₂,х₃. Среди этих наборов необхо­димо выбрать те, которые удовлетворяют всем ограничениям, а из них выбрать набор, при котором функция L(x₁,x₂,х₃) принимает максимальное значение. При n=4 необходимо проверить уже 16 вариантов и т.д. В общем случае нужно рас­смотреть 2ⁿ вариантов.

Для практического использования может быть пред­ложена процедура, предусматривающая максимальное огра­ничение числа рассматриваемых альтернатив на основе их неформального содержательного анализа, а затем форми­рование лучших комбинаций из оставшихся при помощи ме­тодов математического программирования или перебора.