
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обтекание тел при малых возмущениях⇐ ПредыдущаяСтр 34 из 34
Если плоский равномерный поток газа подвергается малым возмущениям
где Если пренебречь квадратами и произведениями этих величин, то в линейном приближении
где Составляющая скорости возмущения
причем Потенциал скорости при малых возмущениях удовлетворяет уравнению
Рис. 12.6. Распространение малых возмущений в дозвуковом (а), звуковом (б) и сверхзвуковом (в) потоках газа
Если в равномерном потоке газа точка А (рис. 12.6) является источником малых возмущений (малых изменений плотности и давления), то эти возмущения в виде слабой волны распространяются в потоке. В зависимости от скорости потока фронты волн возмущения могут занимать одно из положений, показанных на рис. 12.6. В дозвуковом течении (рис. 12.6, а) фронты волн возмущения представляют собой окружности радиусом При сверхзвуковой скорости потока газа волны возмущений также имеют вид окружностей, но в силу условия 
Течение при дозвуковых скоростях. При ( для коэффициента давления
для коэффициента подъемной силы
где индексом «н» отмечены параметры потока несжимаемой жидкости. Течение при сверхзвуковых скоростях. Линеаризованное уравнение потенциала скорости заменой переменных
имеющему общее решение в переменных
где Два семейства прямых, совпадающих с линиями возмущения линеаризованного потока и описываемых формулой Сверхзвуковое обтекание малого угла, образованного плоскими стенками (рис. 12.7). При таком течении из вершины угла выходит характеристика первого семейства, которая делит область течения на две части: невозмущенную и возмущенную. При обтекании выпуклого угла (рис. 12.7, а) поток ускоряется, а при обтекании вогнутого – замедляется (рис. 12.7, б). Обтекание тонкого профиля с заостренными кромками. Задача может быть приближенно решена на основе линеаризованной теории. При этом плавный контур профиля заменяют ломаным (рис. 12.8) и последовательно решают задачу об изменении параметров потока при переходе через каждую линию возмущения, выходящую из точек излома. В результате получают следующие формулы для коэффициента давления: для верхней поверхности, заданной уравнением
для нижней поверхности, заданной уравнением
где
Рис. 12.7. Схемы обтекания сверхзвуковым потоком малого угла: а – ускорение потока; б – торможение потока
Рис. 12.8. Расчетная схема обтекания тонкого профиля линеаризованным сверхзвуковым потоком газа Коэффициент подъемной силы
Коэффициент волнового сопротивления
где Момент сил давления относительно передней кромки
где
здесь
Косые скачки уплотнения
При торможении сверхзвукового потока могут возникать поверхности разрыва, которые наклонены к вектору скорости под углом, отличным от прямого. Такие разрывы называются косыми скачками уплотнения (рис. 12.8). Расчетная система уравнений косого скачка включает в себя уравнения: неразрывности
количества движения (импульса) в проекции на нормаль к фронту скачка
количества движения в проекции на направление, параллельное фронту скачка,
энергии
Рис. 12.8. Расчетная схема косого скачка уплотнения
Из этой системы выводятся соотношения между параметрами потока за скачком и перед ним: для отношения давлений
отношения плотностей
отношения температур
отношения давлений торможения
разности значений энтропии
(12.108) Последняя формула показывает, что переход через косой скачок не является изоэнтропийным и сопровождается потерями механической энергии. Связь между углом наклона фронта скачка
из которой следует, что кривая
Кроме того, каждому значению
откуда следует, что для каждого значения
Рис. 12.9. Расчетная номограмма косых скачков уплотнения
Номограмма для расчета параметров косых скачков приведена на рис. 12.9.
Вопросы для самопроверки: 1. Какое течение газа называется адиабатным? 2. Что понимается под «идеальным» газом? 3. Что понимается под изоэнтропным течением газа? 4. Какие газодинамические функции описывают адиабатное течение идеального газа? 5. Каковы закономерности изменения параметров одномерного адиабатного течения газа вдоль трубы переменного сечения? 6. Каковы характеристики критического сечения сопла Лаваля? 7. Что понимается под прямым скачком уплотнения и каковы условия его возникновения? 8. Каково предельное уплотнение в прямом скачке? 9. Каким параметром оценивается потеря механической энергии в скачке уплотнения? 10. Каковы соотношения между параметрами газового потока в двух сечениях трубы при его адиабатном течении? 11. Каков характер распространения малых возмущений в дозвуковом, звуковом и сверхзвуковом потоках газа? 12. Что понимается под косым скачком уплотнения?
Заключение
Рассмотренные выше общие законы и уравнения статики и динамики жидкостей и газов, вопросы подобия гидромеханических процессов, схемы применения численных методов и их реализация на ЭВМ, по мнению авторов издания, являются базой для изучения ряда дисциплин профессионального цикла, имеющих важное прикладное значение. Указанные теоретические аспекты позволяют выполнять расчеты и проектирование гидромашин, гидроприводов, водо-, газо-, теплоснабжения и других сложных инженерных систем, работа которых основана на законах гидрогазодинамики. Конспект лекций является теоретической основой для изучения дисциплин «Гидрогазодинамика» и «Механика жидкости и газа» студентами бакалавриата направлений 13.03.01 «Теплоэнергетика и теплотехника», 15.03.01 «Машиностроение», 15.03.02 «Технологические машины и оборудование», 20.03.01 «Техносферная безопасность» и будущими инженерами по специальности 08.05.01 «Строительство уникальных зданий и сооружений». Кроме того, базовая часть издания, связанная с рассмотрением законов гидростатики и гидродинамики, может быть использована при изучении дисциплины «Гидравлика» студентами других технических направлений, реализуемых в вузе. При проектировании курса на основе представленных лекционных занятий разрабатываются лабораторно-практические задания, материалы для самоконтроля и промежуточного контроля степени освоения материала. В процессе обучения создаются образовательные ситуации, в которых студенты решают практические задачи в индивидуальной и групповой работе, то есть реализуется методологическая технология проектного обучения с использованием ЭВМ. Кроме того, используются технологии организации самостоятельной работы и балльно-рейтинговой оценки результатов обучения. Список литературы
1. Давидсон, В. Е. Основы гидрогазодинамики в примерах и задачах/ В. Е. Давидсон. – М.: Академия, 2008. – 319 с. 2. Жуков, Н. П. Гидрогазодинамика: учебное пособие/ Н. П. Жуков. – Тамбов: Изд-во ФГБОУ ВПО «ТГТУ», 2011. – 92 с. 3. Касилов, В. Ф. Справочное пособие по гидрогазодинамике для теплоэнергетиков/ В. Ф. Касилов. – М.: Изд-во МЭИ, 2000. – 272 с. 4. Кудинов, А. А. Гидрогазодинамика: учебное пособие/ А. А. Кудинов. – М.: НИЦ ИНФРА-М, 2015. – 336 с. 5. Моргунов, К. П. Гидравлика: учебник/ К. П. Моргунов. – СПб.: Лань, 2014. – 276 с. 6. Теоретические основы теплотехники. Теплотехнический эксперимент: справочник: в 2 кн. Кн. 2. Теплоэнергетика и теплотехника/ под ред. А. В. Клименко, В. М. Зорина. – М.: Изд-во МЭИ, 2001. – 564 с. 7. Штеренлихт, Д. В. Гидравлика/ Д. В. Штеренлихт. – 3-е изд., перераб. и доп. – М.: КолосС, 2005. – 655 с. Оглавление
Учебное издание
ПОЗДЕЕВ Анатолий Геннадиевич КУЗНЕЦОВА Юлия Анатольевна
ГИДРОГАЗОДИНАМИКА
Конспект лекций
Редактор Л. С. Журавлева Компьютерный набор и верстка Ю. А. Кузнецова Дизайн обложки Е. А. Рыбакова
Подписано в печать 29.12.2014. Формат 60х84 1/16 Бумага офсетная. Усл. печ. л. 9,78:
Поволжский государственный технологический университет 424000 Йошкар-Ола, пл. Ленина, 3
Редакционно-издательский центр Поволжского государственного технологического университета
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 500. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 , то при направлении оси
, то при направлении оси 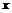 вдоль вектора
вдоль вектора  можно записать
можно записать ;
;  , (12.81)
, (12.81) ,
,  – проекции скорости возмущенного движения.
– проекции скорости возмущенного движения. ; (12.82)
; (12.82) ; (12.83)
; (12.83) ; (12.84)
; (12.84) , (12.85)
, (12.85) – коэффициент давления.
– коэффициент давления. , (12.86)
, (12.86)
 (12.87)
(12.87)
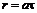 , смещаемые вниз по течению на расстояние
, смещаемые вниз по течению на расстояние  , где
, где 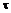 – время с момента возникновения возмущения.
– время с момента возникновения возмущения. область их распространения ограничивается прямыми AM и AN (для осесимметричного потока – поверхностью конуса), называемыми линиями возмущения, или линиями Маха. Эти прямые образуют с вектором скорости угол Маха, определяемый формулой
область их распространения ограничивается прямыми AM и AN (для осесимметричного потока – поверхностью конуса), называемыми линиями возмущения, или линиями Маха. Эти прямые образуют с вектором скорости угол Маха, определяемый формулой . (12.88)
. (12.88) ) замена переменных
) замена переменных  приводит уравнение для потенциала скорости к уравнению Лапласа
приводит уравнение для потенциала скорости к уравнению Лапласа  , т.е. к уравнению, которому удовлетворяет потенциал скорости несжимаемой жидкости. Поэтому при обтекании дозвуковым потоком газа тонкого профиля с малым углом атаки задача приводится к задаче обтекания профиля несжимаемой жидкостью. Формулы пересчета согласно теории Прандтля - Глауэрта имеют вид:
, т.е. к уравнению, которому удовлетворяет потенциал скорости несжимаемой жидкости. Поэтому при обтекании дозвуковым потоком газа тонкого профиля с малым углом атаки задача приводится к задаче обтекания профиля несжимаемой жидкостью. Формулы пересчета согласно теории Прандтля - Глауэрта имеют вид: ; (12.89)
; (12.89) , (12.90)
, (12.90) ,
,  приводится к уравнению гиперболического типа
приводится к уравнению гиперболического типа , (12.91)
, (12.91)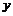 :
: , (12.92)
, (12.92)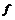 ,
, 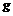 – произвольные функции.
– произвольные функции. , являются характеристиками уравнения (12.91).
, являются характеристиками уравнения (12.91). ,
, ; (12.93)
; (12.93) ,
, , (12.94)
, (12.94)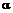 – угол атаки (рис. 12.8).
– угол атаки (рис. 12.8).

 (12.95)
(12.95) , (12.96)
, (12.96) ;
;  ;
;  ;
;  , причем
, причем  – максимальная толщина профиля;
– максимальная толщина профиля; 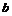 – его хорда.
– его хорда. , (12.97)
, (12.97) – коэффициент момента,
– коэффициент момента, , (12.98)
, (12.98) – коэффициент момента при нулевом угле атаки,
– коэффициент момента при нулевом угле атаки, ; (12.99)
; (12.99) – площадь, равная
– площадь, равная  .
. ; (12.100)
; (12.100) ; (12.101)
; (12.101) или
или  ; (12.102)
; (12.102)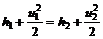 . (12.103)
. (12.103)
 ; (12.104)
; (12.104) ; (12.105)
; (12.105) ; (12.106)
; (12.106) ; (12.107)
; (12.107) .
. и углом поворота потока в скачке
и углом поворота потока в скачке  определяется формулой
определяется формулой , (12.109)
, (12.109) имеет максимум, т.е. существует угол наклона скачка
имеет максимум, т.е. существует угол наклона скачка  , соответствующий максимально возможному отклонению потока в скачке
, соответствующий максимально возможному отклонению потока в скачке  . Значения
. Значения  . (12.110)
. (12.110) связана со скоростью
связана со скоростью  перед скачком соотношением
перед скачком соотношением , (12.111)
, (12.111) , при котором
, при котором  . При
. При  поток за скачком остается сверхзвуковым (слабые скачки), при
поток за скачком остается сверхзвуковым (слабые скачки), при  он будет дозвуковым (сильные скачки). Для определения
он будет дозвуковым (сильные скачки). Для определения  служит уравнение
служит уравнение (12.112)
(12.112)

