
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Адиабатное течение невязкого идеального газаАдиабатным называют течение, происходящее без теплообмена с внешней средой. Газ рассматривается как «идеальный», если он подчиняется уравнению состояния Клапейрона - Менделеева
При одномерном течении все параметры газа зависят только от одной геометрической координаты:
Во многих случаях влиянием силы тяжести пренебрегают. Вводя в рассмотрение энтальпию
где
Поскольку
Вводя скорость звука
При адиабатном течении невязкого газа (
сохраняет постоянное значение, из-за чего течение называется изоэнтропным. Характерные параметры такого течения: параметры торможения критическая скорость максимальная скорость Правая часть может быть выражена через эти параметры:
Критическая скорость
Употребительны безразмерные скорости:
Использование уравнений процесса 
При изоэнтропном течении параметры торможения во всех точках имеют одно и то же значение, поэтому для двух сечений одномерного потока справедливы соотношения:
Полагая
Газодинамические функции
Если газовый поток с местными параметрами Помимо функций
представленных на рис. 12.1, употребительны также другие газодинамические функции. Например, использовав функцию приведенного расхода газа
можно рассчитать массовый расход газа через сечение
где сомножитель
Использовав функцию
для массового расхода газа можно получить следующее выражение:
Графики функций
Рис. 12.1. Графики газодинамических функций
Функции
При использовании уравнения импульса газа вводится понятие полного импульса, которое может быть выражено в следующих видах:
где
Графическое представление газодинамических функций и дано на рис. 12.2. Более точные, чем по этим графикам, значения функций можно получить с помощью таблиц, приводимых в руководствах по газовой динамике.
Рис. 12.2. Графики газодинамических функций Изменение параметров одномерного адиабатного |
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 606. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
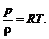 (12.1)
(12.1)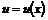 ;
; 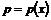 ;
; 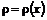 . (12.2)
. (12.2)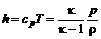 , (12.3)
, (12.3)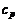 – удельная теплоемкость при постоянном давлении, уравнение адиабатного течения невязкого газа представляем в виде
– удельная теплоемкость при постоянном давлении, уравнение адиабатного течения невязкого газа представляем в виде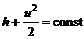 . (12.4)
. (12.4)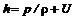 , где
, где 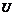 – внутренняя энергия, уравнение принимает вид
– внутренняя энергия, уравнение принимает вид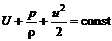 . (12.5)
. (12.5)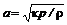 , получаем
, получаем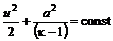 . (12.6)
. (12.6)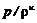 = const) энтропия
= const) энтропия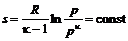 (12.7)
(12.7)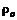 ,
, 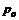 ,
, 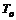 ,
, 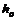
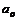 , т.е. значения параметров
, т.е. значения параметров 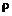 ,
,  ,
,  ,
, 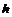 ,
, 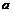 , а в точке или сечении потока, где газ полностью обратимо заторможен:
, а в точке или сечении потока, где газ полностью обратимо заторможен: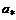 , т.е. значение скорости
, т.е. значение скорости  , равное местной скорости звука;
, равное местной скорости звука;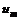 , т.е. значение скорости газа при его истечении в пустоту.
, т.е. значение скорости газа при его истечении в пустоту.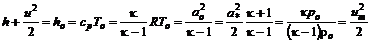 . (12.8)
. (12.8)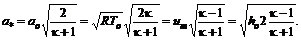 (12.9)
(12.9)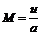 ;
; 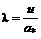 ;
; 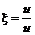 . (12.10)
. (12.10)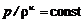 и состояния
и состояния 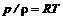 позволяет получить формулы для отношений давлений, плотностей, температур:
позволяет получить формулы для отношений давлений, плотностей, температур: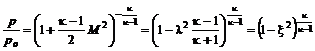 ; (12.11)
; (12.11)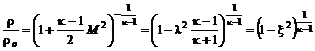 ; (12.12)
; (12.12)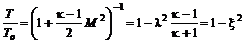 . (12.13)
. (12.13)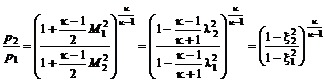 ; (12.14)
; (12.14)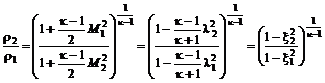 ; (12.15)
; (12.15)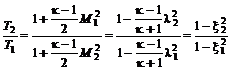 . (12.16)
. (12.16)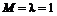 или
или 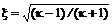 получаем критическое отношение соответствующих параметров:
получаем критическое отношение соответствующих параметров: 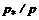 ;
; 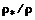 ;
; 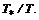
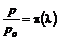 ;
; 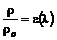 ;
; 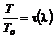 , (12.17)
, (12.17)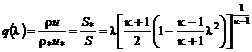 , (12.18)
, (12.18) :
: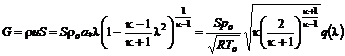 , (12.19)
, (12.19) имеет следующие значения:
имеет следующие значения: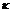
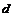
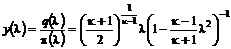 , (12.20)
, (12.20)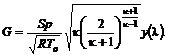 (12.21)
(12.21)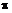 ,
,  ,
, 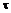 ,
, 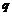 для
для 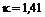 приведены на рис. 12.1.
приведены на рис. 12.1.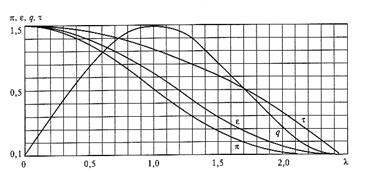
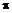 ,
, 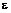 ,
, 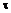 ,
, 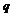 (
( 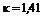 )
)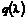 и
и 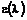 связаны соотношением
связаны соотношением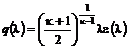 . (12.22)
. (12.22)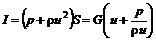 ; (12.23)
; (12.23)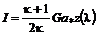 ; (12.24)
; (12.24)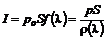 , (12.25)
, (12.25)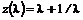 ;
; 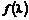 ;
; 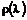 – газодинамические функции, определяемые формулами:
– газодинамические функции, определяемые формулами: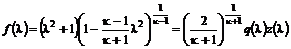 ; (12.26)
; (12.26)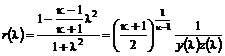 . (12.27)
. (12.27)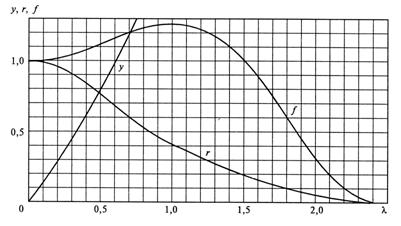
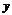 ,
, 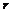 ,
, 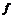 (
( 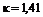 )
)