
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вихревые линии и вихревые трубки
Вихри скоростей образуют вихревое поле, в котором находятся вихревые линии и вихревые трубки. Из определения вихревой линии и вихревой трубки следует, что в любой точке таких линий и поверхностей нормальная составляющая вихря скорости равна нулю. Вводя понятие потока вектора вихря скорости, равного
где
Поток вектора вихря скорости сквозь произвольное поперечное сечение вихревой трубки в данный момент времени одинаков вдоль всей трубки (рис. 5.4):
Рис. 5.4. Вихревая трубка
Это утверждение составляет вторую теорему Гельмгольца. Поток вихря характеризует интенсивность вихревой трубки
При постоянной величине вихря
откуда следует: 1) сечение вихревой трубки нигде не может стать равным нулю, т.к. бесконечно большая скорость вращения частиц физически невозможна; 2) вихревые трубки не могут заканчиваться внутри жидкости: они либо замыкаются на себя, образуя вихревые кольца, либо «опираются» на стенку или на свободную поверхность. Другой важной теоремой о вихрях является теорема Стокса: интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, один раз опоясывающему вихревую трубку, т.е.
где
Безвихревое движение жидкости.  Интегралы Коши-Лагранжа и Бернулли Для потенциального движения
Если во всей области движения жидкости
где величина ротора скорости
где
или Уравнение Эйлера в форме Громеки - Ламба имеет вид
или в векторной форме
Условие потенциальности позволяет записать
Следовательно, выражение в скобках зависит только от времени, поэтому интеграл уравнения будет иметь вид
где Когда массовые силы сводятся силами тяжести, потенциал которых
В этом уравнении имеются два неизвестных
или
Решение последнего уравнения Лапласа позволяет найти потенциал скорости
определяет давление Для стационарного движения Это интеграл Бернулли для потенциальной струйки идеальной несжимаемой жидкости. Наиболее употребительна его форма вида
где
Кинематика вихревых колец
Для модели циркуляционного течения (рис. 5.5) по любой из концентрических окружностей с центром в начале координат циркуляция скорости равна
где
Рис. 5.5. Кинематика плоского вихря
Отсюда скорость, индуцируемая прямолинейным вихрем в плоскости, расположенной по нормали к его оси, будет
Для вихревого кольца радиусом R (рис. 5.6) индуцированная скорость в идеальной жидкости по закону Био-Савара направлена по оси аппликат
а компоненты
Рис. 5.6. Кинематика вихревого кольца
В вязкой среде происходит диссипация энергии, и величина завихренности во времени
где Вектор угловой скорости вращения частицы имеет вид
а его проекции на оси координат равны
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 615. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (5.10)
, (5.10) – площадь поверхности;
– площадь поверхности; 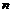 – нормаль к поверхности, найдем, что поток вектора вихря скорости через вихревую поверхность будет равен нулю:
– нормаль к поверхности, найдем, что поток вектора вихря скорости через вихревую поверхность будет равен нулю: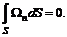 (5.11)
(5.11)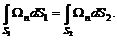 (5.12)
(5.12)

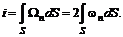 (5.13)
(5.13)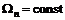 получим
получим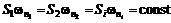 , (5.14)
, (5.14)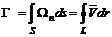 , (5.15)
, (5.15)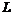 – длина контура.
– длина контура.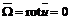 или
или 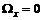 ,
, 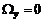 ,
, 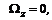 (5.16)
(5.16)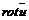 определяется с применением оператора набла (
определяется с применением оператора набла ( 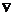 ) в виде
) в виде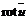 =
= 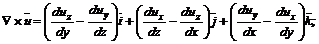 (5.17)
(5.17)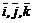 – орты (единичные векторы) осей декартовой системы координат в направлениях X, Y, Z соответственно, то существует потенциал скорости
– орты (единичные векторы) осей декартовой системы координат в направлениях X, Y, Z соответственно, то существует потенциал скорости 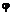 и скорость имеет компоненты, определяемые следующим образом:
и скорость имеет компоненты, определяемые следующим образом: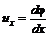 ;
; 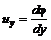 ;
; 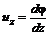 (5.18)
(5.18)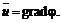
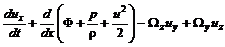 ;
;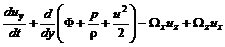 ; (5.19)
; (5.19)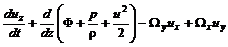
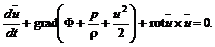 (5.20)
(5.20)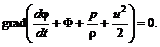 (5.21)
(5.21)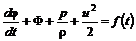 , (5.22)
, (5.22)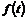 определяется из краевых условий. Этот интеграл уравнения Эйлера называется интегралом Коши-Лагранжа для потенциального движения идеальной несжимаемой жидкости.
определяется из краевых условий. Этот интеграл уравнения Эйлера называется интегралом Коши-Лагранжа для потенциального движения идеальной несжимаемой жидкости.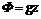 , интеграл Коши-Лагранжа принимает вид
, интеграл Коши-Лагранжа принимает вид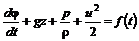 . (5.23)
. (5.23) , поэтому следует использовать уравнение неразрывности
, поэтому следует использовать уравнение неразрывности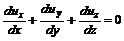 (5.24)
(5.24)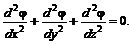 (5.25)
(5.25)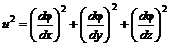 (5.26)
(5.26)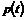 в некоторой точке.
в некоторой точке.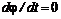 и с учетом выражения потенциала массовой силы тяжести
и с учетом выражения потенциала массовой силы тяжести 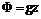 получим
получим 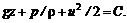
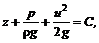 (5.27)
(5.27) – геометрическая высота (удельная потенциальная энергия) положения сечения струйки;
– геометрическая высота (удельная потенциальная энергия) положения сечения струйки; 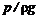 – пьезометрическая высота (удельная потенциальная энергия давления);
– пьезометрическая высота (удельная потенциальная энергия давления); 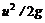 – скоростной напор (удельная кинетическая энергия).
– скоростной напор (удельная кинетическая энергия).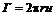 , (5.28)
, (5.28)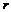 – радиус соответствующей окружности.
– радиус соответствующей окружности.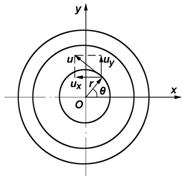
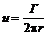 . (5.29)
. (5.29)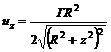 , (5.30)
, (5.30)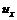 и
и 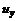 равны нулю.
равны нулю.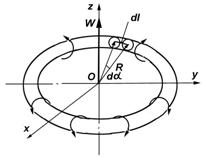
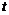 равна
равна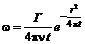 , (5.31)
, (5.31) – коэффициент кинематической вязкости.
– коэффициент кинематической вязкости.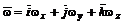 , (5.32)
, (5.32)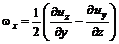 ;
;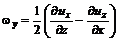 ; (5.33)
; (5.33)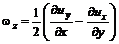 .
.