
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Особенности движения жидкой частицы
Теорема Коши-Гельмгольца гласит, что скорость в каждой точке элементарного объема жидкости складывается из скоростей поступательного движения вместе с полюсом, вращательного движения вокруг полюса и деформационного движения (рис. 3.6):
Рис. 3.6. Движение жидкого объема
Первые два члена Если положение точки А относительно полюса определяется вектором
Разложение в ряд Тейлора непрерывной функции координат
Аналогичные соотношения можно получить и для двух других компонентов скорости Введем двучлен вида
Величина Величины
являются компонентами угловой скорости вращения частицы вокруг полюса. Кроме квазитвердого движения частицы происходит деформационное движение ее частей, о чем говорят члены
Для пояснения их физического смысла рассмотрим движение отрезка в жидкости В момент
то есть отрезок растянется или сожмется.
т. е.  При движении отрезка
Рис. 3.7 Деформация жидкой линии: а – вдоль оси х; б – вдоль оси z
Если одновременно движутся два отрезка Деформация прямого угла равна
где
Ускорение жидкой частицы
Проекции ускорения
Величины производных от координат по времени могут быть переписаны как
поэтому
Аналогичные соотношения можно получить и для функций Слагаемые Компоненты Уравнениям для проекции ускорения на ось
можно придать вид
Конвективные составляющие уравнения содержат члены типа В ряде случаев используется понятие завихренности жидкости с компонентами
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 744. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
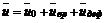 . (3.16)
. (3.16)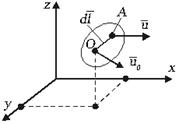
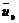 и
и 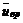 характерны и для движения твердой частицы, поэтому их можно трактовать как скорость квазитвердого движения.
характерны и для движения твердой частицы, поэтому их можно трактовать как скорость квазитвердого движения.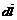 , то векторы
, то векторы 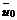 ,
, 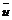 и
и 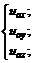

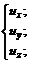
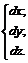 (3.17)
(3.17)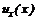 в точке полюса
в точке полюса 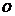 с точностью первого порядка малости дает
с точностью первого порядка малости дает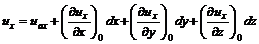 . (3.18)
. (3.18)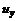 и
и 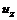 .
.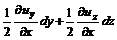 , прибавляя и вычитая который из последнего равенства, запишем
, прибавляя и вычитая который из последнего равенства, запишем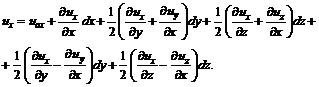 (3.19)
(3.19)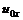 характеризует поступательное движение полюса.
характеризует поступательное движение полюса.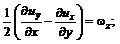
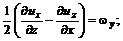
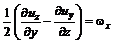 (3.20)
(3.20)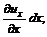
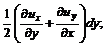
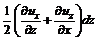 . (3.21)
. (3.21)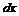 вдоль оси
вдоль оси 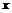 (рис. 3.7, а).
(рис. 3.7, а).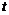 скорость начала отрезка
скорость начала отрезка 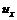 . Скорость его конца при разложении по формуле Тейлора будет
. Скорость его конца при разложении по формуле Тейлора будет 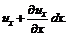 За время
За время 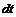 отрезок продвигается влево, но его концы пройдут расстояния
отрезок продвигается влево, но его концы пройдут расстояния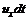 и
и 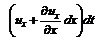 , (3.22)
, (3.22)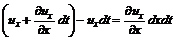 , (3.23)
, (3.23)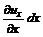 есть линейная деформация отрезка за время
есть линейная деформация отрезка за время 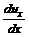 является скоростью относительной линейной деформации.
является скоростью относительной линейной деформации.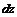 вдоль оси
вдоль оси  (рис. 3.7, б) его концы имеют скорости
(рис. 3.7, б) его концы имеют скорости 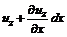 и за время
и за время 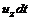 и
и 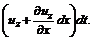 В результате за время
В результате за время 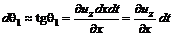 . (3.24)
. (3.24)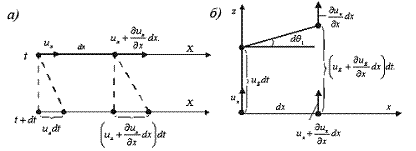
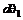 , а отрезок
, а отрезок 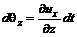 .
.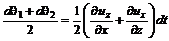 , (3.25)
, (3.25)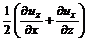 – скорость деформации прямого угла.
– скорость деформации прямого угла.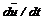 жидкой частицы на оси x, y, z будут иметь вид
жидкой частицы на оси x, y, z будут иметь вид 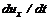 ,
, 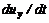 и
и 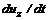 . Для проекции производной скорости на ось
. Для проекции производной скорости на ось 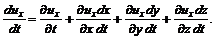 (3.26)
(3.26)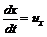 ;
; 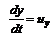 ;
; 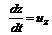 , (3.27)
, (3.27)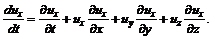 (3.28)
(3.28)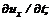
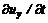 ;
; 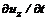 являются локальными ускорениями в данной точке жидкости.
являются локальными ускорениями в данной точке жидкости.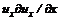 ,
, 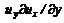 ,
, 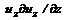 характеризуют изменение компонент скорости при прохождении частицы через данную точку и называются конвективными ускорениями.
характеризуют изменение компонент скорости при прохождении частицы через данную точку и называются конвективными ускорениями.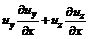 (3.29)
(3.29)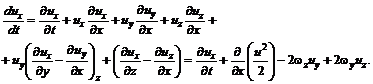 (3.30)
(3.30)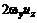 , ответственные за вращение (завихрение) жидкости.
, ответственные за вращение (завихрение) жидкости.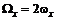 ,
, 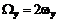 ,
, 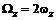 .
.