
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Собственные вектора и собственные числа. ⇐ ПредыдущаяСтр 8 из 8 Опр1.Ненулевой вектор х в L называют собственным вектором линейного оператора А:L→ L, если для некоторого действительного числа λ выполняется соотношение Ах= λх. При этом число λ называют собственным значением (собственным числом) линейного оператора А. Ах=λх=λЕх,
Собственный вектор х находится из однородной системы уравнений . Собственные вектора существуют, если det(A-λE)=0. Это уравнение называется характеристическим уравнением оператора А(х), заданного матрицей А в базисе е1,…,en. Утверждение. Характеристическое уравнение не зависит от выбора базиса. ◄ пусть е´ новый базис. S матрица перехода от базиса е к е´. Тогда det(A-λE)= Определение. Собственные числа – решение характеристического уравнения det(A-λE)=0 det
Следовательно, что характеристическое уравнение является многочленом от λ, а собственные числа есть корни этого многочлена. det(A-λE)=(а11- λ)(а22- λ)…(аnn- λ)+..= Предположим λ=0, det(A-0E)= detA=Ао. Наше характеристическое уравнение примет вид Многочлен в (2) называется характеристическим многочленом матрицы А
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 423. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
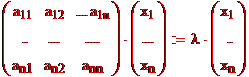 =
= 
 , отсуда (А-λЕ)х=0
, отсуда (А-λЕ)х=0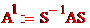 , где А´ - матрица оператора А(х) в базисе е´
, где А´ - матрица оператора А(х) в базисе е´ = =
= = 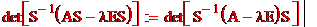 =det
=det 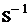 *det(A-λE)*detS= det(A-λS)►
*det(A-λE)*detS= det(A-λS)►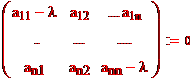 Известно, что определитель матрицы есть алгебраическая сумма произведений n различных элементов матрицы.
Известно, что определитель матрицы есть алгебраическая сумма произведений n различных элементов матрицы.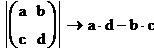
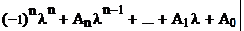 (1)
(1)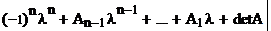 =0
=0