
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Миноры. Алгебраические дополнения. Разложение определителя по элементам строки (столбца)Стр 1 из 8Следующая ⇒ Высшая алгебра и аналитическая геометрия Матрицы, операции над ними. Определитель, свойства определителей. Нахождение обратной матрицы. Ранг матрицы. Матрица и действия с матрицами Опр.Таблица чисел
Опр.Суммой двух матриц Опр.Произведение матрицы Очевидно, что выполняются следующие свойства операций: 1)А+В=В+А; 2) (А+В)+С=А+(В+С); 3)( Здесь А, В, С – любые матрицы одинаковой размерности, Опр.Множества, в которых введены 2 операции, связанные свойствами 1)-8) называются линейными пространствами. Итак, множество матриц одинаковой размерности образует линейное пространство с определенными выше операциями. Опр.Произведением матриц Замечание.Определение корректно (имеет смысл) только тогда, когда число столбцов матрицы А равно числу столбцов строк матрицы В. Уже в числу этого умножение не обладает свойством коммутативности: АВ Пример:Найти произведение матриц и проверить перестановочны ли они.
Произведение ВА не имеет смысла. Значит, АВ Опр.Матрица n-го порядка Е называется единичной матрицей n-го порядка, если у нее все элементы на главной диагонали равны 1, а остальные равны 0.  Из определения произведения следует, что АЕ=ЕА=А, если А также матрица n-го порядка. Другие свойства операции умножения: 1) (А+В)С=АС+ВС; 2) А(В+С)=АВ+АС; 3) ( 4) (АВ)С=А(ВС); 5) 0А=А0=0, если операции сложения и умножения имеют смысл. Докажем, например, свойство 4). Для элемента i-й строки и k-го столбца (АВ)С имеем (считая
Получили элемент i-ой строки и k-го столбца матрицы А(ВС), что требовалось доказать. Определитель и их свойства Опр.Пусть А – квадратная матрица порядка n. Число
называется определителем матрицы А (другие обозначения: det A, det||aij||), где Заметим, что каждое слагаемое определителя n-го порядка в качестве сомножителей содержит по одному элементу с каждого столбца и с каждой строки; число слагаемых равно числу перестановок из n элементов, т.е. равно n!. Рассмотрим, определите 2-го и 3-го порядка. При n=2 получим
При n=3 имеем
Докажем следующие свойства определителей. 1. При транспонировании (замене строк столбцами с теми же номерами) определитель не меняется местами. Доказательство. Переставим сомножители в каждом слагаемом определителя (1) так, чтобы вторые индексы давали перестановку (1, 2, …, n). Получим произведение Сложив (1) и (2) и поделив на 2 получим
Отсюда видно, что
Действительно, каждое слагаемое в (1) содержит сомножитель из нулевой строки, равный нулю, поэтому |A|=0. 2. Если в определителе поменять местами две строки (столбца), то он поменяет знак. Доказательство. Если переставим k-ю и s-ю строку, то вместе слагаемого 3. Определитель с двумя одинаковыми строками (столбцами) равен нулю. Действительно, если переставить одинаковые строки, то определитель не меняется. С другой стороны, в силу свойства 3, определитель меняет знак. Значит, |A|= -|A|. Отсюда, |A|=0. 4. Если элементы какой-либо строки (столбца) умножить на число 5. Если элементы k-й строки (столбца) определителя имеют вид 6. Если к строке (столбцу) прибавить другую строку (столбец), умноженную на какое-либо число, то определитель не изменяется. Для доказательства к новому определению применяем свойства 6, 5, 4. Миноры. Алгебраические дополнения. Разложение определителя по элементам строки (столбца) Опр.Определитель матрицы, получаемой при вычеркивании матрицы А нескольких строк и столбцов, называется минором матрицы А. Очевидно, что надо вычеркивать столько строк и столбцов, чтобы оставшаяся матрица была квадратной, иначе нельзя найти ее определитель. Если матрица А была квадратной, то вычеркиваются одинаковое число строк и столбцов. Если вычеркиваем i-ю строку и j-й столбец, то минор обозначается Мij и называется минором элемента аij, стоящего на пересечении i-й строки и j-го столбца. Опр.Число Аij=(-1)i+jMij называется алгебраическим дополнением элемента аij . Теорема.Если Доказательство. 1. Рассмотрим сначала случай
т.е.
2. Рассмотрим случай 3. Общий случай. Представим определитель |A| как сумму определителей |Ak| таких, что у всех определителей строки, за исключением i-й строки, совпадают со строками определителя |A|. Для определителя |Ak| i-я строка имеет вид (0, …, 0, aik, 0,…, 0). Используя предыдущий случай, получим
что требовалось доказать. Замечание.Определитель можно разлагать и по элементам столбца. Следствие.Сумма произведений элементов строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю. Доказательство. Действительно, сумма Пример.Найти определитель Разлагаем по элементам 1-го столбца. Получим |A|=2(-1)1+1 Обратная матрица Опр.Пусть А – матрица n-го порядка. Матрица А-1 называется обратной к А, если А-1А=АА-1=Е. если существует А-1, то А называется обратимой. Замечание.Если А-1 существует, то она единственная. Действительно, пусть А’ другая, обратная к А. тогда умножая А-1А=Е на А’ справа получим (А-1А)А’=ЕА’ Теорема.А-1 существует тогда и только тогда, когда det A Док-во.Необходимость. Дано, что А-1 существует. Тогда АА-1=Е Достаточность. Дано, что |A|
имеет вид
При i=k в числителе имеем разложение |A| по k-й строке, поэтому сkk=
Пример.Найти А-1, если она существует, А= Имеем |A|= -3+6+0-8-2-0= -7
А21= -(-2)=2, А22=11, А23= -1, А31=2, А32= -(-4)=4, А33= -1. Тогда присоединенная матрица имеет вид
Транспонируем
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 510. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
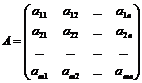 называется числовой матрицей размерности m
называется числовой матрицей размерности m 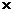 n, числа
n, числа 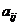 - элементами матрицы А. Если m=n, то матрица называется квадратной матрицей порядка n. Рассмотрим множество матриц размерности m
- элементами матрицы А. Если m=n, то матрица называется квадратной матрицей порядка n. Рассмотрим множество матриц размерности m 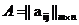 и
и 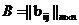 называется матрица
называется матрица 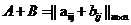 .
.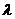 называется матрица
называется матрица 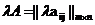 .
.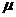 А)=(
А)=( 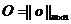 такой, что А+О=А; 8)существует противоположный элемент
такой, что А+О=А; 8)существует противоположный элемент 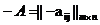 такой, что А+(-А)=О.
такой, что А+(-А)=О.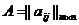 и
и 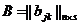 называется матрица
называется матрица 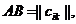 где
где 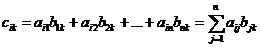 .
.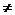 ВА. Перестановочности, вообще говоря, нет и тогда, когда оба произведения имеют смысл.
ВА. Перестановочности, вообще говоря, нет и тогда, когда оба произведения имеют смысл.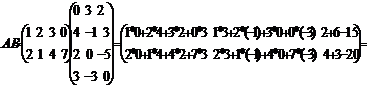 =
= 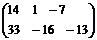
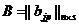 ,
, 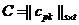 )
)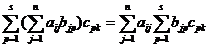 .
.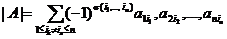 (1)
(1)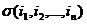 - число инверсий в перестановке
- число инверсий в перестановке 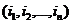 или, что то же самое, в подстановке
или, что то же самое, в подстановке 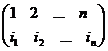 .
.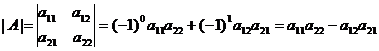 .
.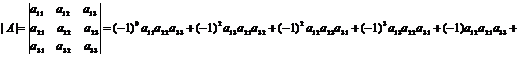
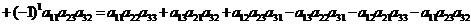 .
.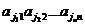 . При этом перестановка
. При этом перестановка 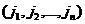 имеет ту же четность что и
имеет ту же четность что и 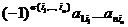 можно писать
можно писать 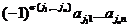 . Но индексы суммирования можно обозначать любыми буквами, поэтому заменяя j на i получим
. Но индексы суммирования можно обозначать любыми буквами, поэтому заменяя j на i получим 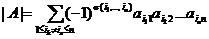 . (2)
. (2)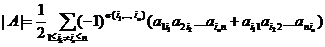 .
.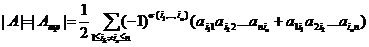 Если определитель содержит нулевую строку (столбец), то он равен нулю.
Если определитель содержит нулевую строку (столбец), то он равен нулю.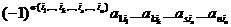 в определителе (1) возникает слагаемое
в определителе (1) возникает слагаемое 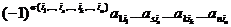 , которое отличается лишь знаком, так как перестановки
, которое отличается лишь знаком, так как перестановки 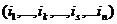 и
и 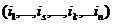 имеют разную четность. Итак, определители также отличаются лишь знаками. Утверждение для столбцов получится, если использовать свойство 1.
имеют разную четность. Итак, определители также отличаются лишь знаками. Утверждение для столбцов получится, если использовать свойство 1.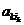 возникает
возникает 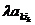 , если умножаются элементы k-й строки. Вынося
, если умножаются элементы k-й строки. Вынося 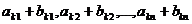 , то он равен сумме двух определителей, которые отличаются от исходного определителя только k-ми строками (столбцами): у одного определителя k-я строка (столбец) состоит из
, то он равен сумме двух определителей, которые отличаются от исходного определителя только k-ми строками (столбцами): у одного определителя k-я строка (столбец) состоит из 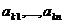 , у другого – из
, у другого – из 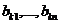 .
.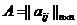 ,
, 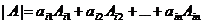 то и это представление называется разложением определителя по элементам i-й строки.
то и это представление называется разложением определителя по элементам i-й строки.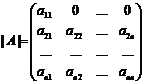 ,
,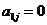 при
при 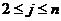 . Тогда
. Тогда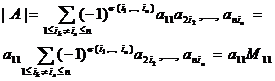
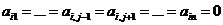 , т.е. в i-й строке только элемент j-го столбца может отличаться от нуля. Тогда i-ю строку переставляя с соседними переводим на первую строку. При этом знак определителя меняется i-1 раз. Далее, j-й столбец переводим на первый столбец, переставляя с соседними столбцами. При этом знак определителя меняется j-1 раз. Итак, учитывая предыдущий случай, получим
, т.е. в i-й строке только элемент j-го столбца может отличаться от нуля. Тогда i-ю строку переставляя с соседними переводим на первую строку. При этом знак определителя меняется i-1 раз. Далее, j-й столбец переводим на первый столбец, переставляя с соседними столбцами. При этом знак определителя меняется j-1 раз. Итак, учитывая предыдущий случай, получим 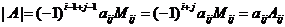 .
.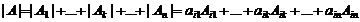 ,
,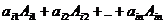 представляет разложение по k- й строке определителя, у которого k-я строка совпала с i-й строкой. А определитель с двумя одинаковыми строками равен нулю.
представляет разложение по k- й строке определителя, у которого k-я строка совпала с i-й строкой. А определитель с двумя одинаковыми строками равен нулю.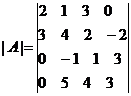 .
.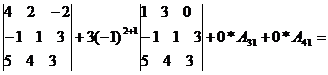 2(12+8+30+10-48+6)-3()3+0+45-0- 12+9=36-135=-99.
2(12+8+30+10-48+6)-3()3+0+45-0- 12+9=36-135=-99.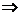 А-1(АА’)=А’
А-1(АА’)=А’ 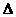 =|A|
=|A| 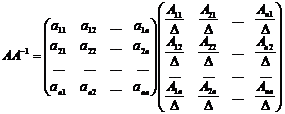
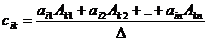 .
.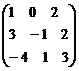 .
. 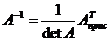

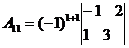 = -5,
= -5, 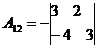 = -17, А13= -1,
= -17, А13= -1, 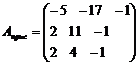 .
.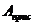 и делим все элементы на |A|= -7. Получим обратную матрицу
и делим все элементы на |A|= -7. Получим обратную матрицу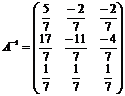 .
.