
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Линейные операторы. Матрица линейного оператора. Ядро и образ линейного оператора. Собственные вектора и собственные числа линейных операторов.Опр.1. Отображением А из линейного пространства L в линейное пространство L΄ называется правило по которому к каждому элементу х из L сопоставляется элемент y из L΄. Опр.2. Отображение А:L→ L΄ из линейного пространства L в линейное пространство Ľ называется линейным отображением или линейным оператором, если выполнены следующие условия: а) А(х+у)=А(х)+А(у) для любых векторов х,у€ L; б)А(λх)=λА(х) для любого вектора х€ L и любого числа λ€R Линейный оператор А:L→L΄, который осуществляет отображение линейного пространства L в себя, называют линейным преобразованием,и говорят что линейный оператор А действует в линейном пространстве L. Из определения линейности отображения вытекает, что для любого линейного оператора А:L→ L΄ образом А0 нулевого вектора в L является нулевой вектор 0΄ в Ľ: А(0)= 0΄. Действительно, А0=А(0*0)=0(А0)= 0΄. Для того чтобы доказать линейность какого-либо отображения линейных пространств, нужно проверить условия а),б) определения 2.Линейный оператор переводит нулевой вектор снова в нулевой, и это свойство может рассматриваться как необходимое условие линейности (но не достаточное). Пример 1. зададим линейное отображение по правилу Â(х)=Ах, т.е. Ах= Â:
=Â(х)+ Â(у)
Пример 2. Отображение А:R→R n-мерного линейного арифметического пространства в себя, которое задается формулой Ах=а+х, где а≠0 – некоторый фиксированный вектор, не является линейным, т.к., например, образом нулевого вектора является вектор а.  Следствие.Любая матрица порядка m×n определяет линейное отображение из L в Ľ. Опр. 3. Каждому линейному оператору А:L→ L΄ соответствуют: · его ядро kerA- множество тех векторов х € L, для которых Ах= 0΄ ,где 0΄-нулевой вектор в L΄; · его образ imA – множество векторов у € L΄, являющихся значениями этого оператора. Теорема1.Для любого линейного оператора А:L→ L΄его ядро kerA является линейным подпространством в L,а его образ imA- линейным подпространством в L΄. ◄Доказательство сводится к проверке условий определения линейного подпространства. Пусть векторы х1 и х2 принадлежат множеству kerA, т.е. Ах1=0΄, Ах2= 0΄.Тогда согласно условию а) определения 2, А(х1+х2)=Ах1+Ах2=0΄+ 0΄= 0΄, т.е.вектор х1+х2 принадлежит множеству kerA, а, согласно условию б) того же определения, для любого действительного числа λ А(λх1)= λ(Ах1)= λ0΄= 0΄, т.е. и вектор λх1 принадлежат kerA. Как видим, множество kerA замкнуто относительно линейных операций и потому является линейным подпространством. Если векторы у1 и у2 принадлежат множеству imA, то существуют такие векторы х1,х2 € L, что у1=Ах1,у2=Ах2. Но тогда, согласно условию а) определения2, у1+у2=Ах1+Ах2=А(х1+х2), т.е. вектор у1+у2 является значением оператора А и, следовательно, принадлежат imA. Аналогично вектор λу1= λ(ах1)=А(λх1) также входит в множество imA для любого λ €R. Приходим к выводу, что и imA является линейным подпространством, но уже в лин. пространстве L΄.► Размерность ядра и образа – важнейшие характеристики линейного оператора. Число dim(kerA) называют дефектом линейного оператора А, а число dim(imA) – его рангом. Среди линейных операторов, отображающих линейное пространство L в себя есть два важных частных случая: тождественный оператор I, который каждый вектор переводит в себя (Ix=x), и нулевой оператор Θ,который каждый вектор отображает в нулевой (Θх=0). Эти два оператора являются предельными с точки зрения дефекта и ранга. Нулевой оператор имеет максимальный дефект (равный dimL) и минимальный ранг (нулевой). Тождественный оператор, наоборот, имеет минимальный дефект (нулевой) и максимальный ранг (равный dimL).Оператор максимального дефекта определен однозначно, а операторов минимального дефекта и максимального ранга бесконечно много. Отображение, при котором различные векторы имеют различные образы, называется инъективным отображением. Отображение инъективно тогда и только тогда, когда его ядро – нулевое подпространство. Если отображение инъективно, то линейно независимые векторы переходят в линейно независимые. Действительно, пусть образы векторов х1,…,хк линейно зависимы: α1А(х1)+…+αкА(хк)=0. Тогда А(α1х1+…+αкхк)=0. отсюда для инъективного отображения получаем α1х1+…+αкхк=0, и, следовательно,х1,…,хк линейно зависимы. Матрица линейного оператора. Пусть А- линейный оператор. А(х)=у, х€L, у€L´, е1,…,еn- базис в L, а h1,…,hm – базис в L´ е1,…,еn относятся в h1,…,hm , А(е1) €L´,
………………………………
рассмотрим матрицу линейного оператора а(х):
Замечание1. i – столбец А есть координаты А(ei) в базисе L´
=
…………………………
Замечание2. Линейный оператор А(х) действует по правилу А(х)=Ах, где А – матрица линейного оператора. Замечание 3. Каждый линейный оператор А можно сопоставить матрицу А: А(х)=Ах с другой стороны каждая матрица А m×n соответствует линейному оператору А(х)=Ах из L Т.о. между линейным оператором из L в L´ и матрицы m×n существует взаимнооднозначное соответствие в базисах е1,…,еn, h1,…,hm, т.е. если есть лин.оператор. Связь между матрицами линейного оператора в различных базисах. Рассмотрим А:L→ L΄. Пусть е1,…,еn – базис в L, h1,…,hm- базис в L´. Нашему линейному оператору А(х) соответствует матрица А: А(х)=Ах Тогда следует ожидать, что при замене базиса матрица А меняется.
Пусть Пусть Р – матрица перехода Тогда для любого х €L А(х)=Ах=у €L´,где Следовательно, х=Sx´, y=Py´ А Sx´=Ру´, С другой стороны мы ищем матрицу А´: А´х´=у´. Следовательно,
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 536. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
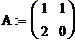
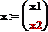
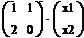
 →
→ 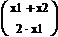 ,
, 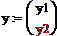
 =
=  =
= 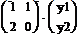 =
=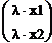 =λА
=λА 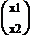 =λÂ(х)
=λÂ(х) 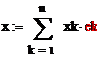 ,
, 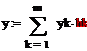
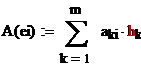
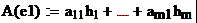


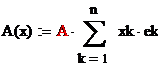 =
= 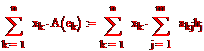
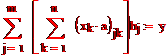 =
=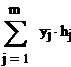
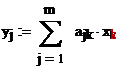 =
= 
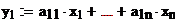
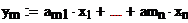
 базис в L,
базис в L,  базис в L´
базис в L´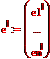 новый базис в L. S – матрица перехода от старого базиса к новому, т.е.
новый базис в L. S – матрица перехода от старого базиса к новому, т.е. 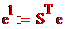
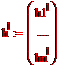 новый базис в L´
новый базис в L´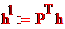 .
.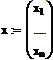 ,
,  Пусть
Пусть 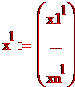 координаты х в новом базисе,
координаты х в новом базисе, 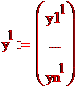 координаты у в новом базисе
координаты у в новом базисе .
.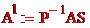 - закон изменения матрицы А при переходе к новому базису или иначе, связь между матрицами.
- закон изменения матрицы А при переходе к новому базису или иначе, связь между матрицами.