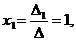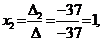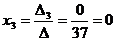Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы нахождения ранга матрицы.1-й способ: Доказательство теоремы о ранге матрицы дает метод нахождения ранга с помощью окаймляющих миноров. Если найдется минор r-го порядка, отличный от нуля, а все окаймляющие его миноры (r+1)-порядка равны нулю, то ранг матрицы равен r. Пример.Найдем ранг матрицы А= Минор Окаймляющий минор Другой окаймляющий минор Окаймляющий минор Других миноров 4-го порядка нет. Значит, r<4. Тогда к=3. 2-й способ: В силу теоремы ( Если Пример: А= Система линейных алгебраических уравнений. Метод Гаусса. Метод Крамера. Фундаментальная система решений однородной системы линейных алгебраических уравнений. Опр.Система
называется СЛУ из m уравнений с n неизвестными Опр.Упорядоченный набор чисел (с1,…,сn) называется решением системы (1), если при подстановке в систему (1) эти числа превращают уравнения в верные равенства. Опр.Если решений нет, то система называется несовместной (противоречивой); если существует бесконечно много решений, то система называется неопределенной; если существует единственное решение, то определенной.  Опр. Две системы называются эквивалентными, если они имеют одинаковое множество решений. Следующие преобразования системы называются элементарными: 1) перестановка местами двух уравнений; 2) отбрасывание из системы уравнений вида 3) умножение обеих частей какого-либо уравнения на число, отличное от нуля; 4) прибавление к одному из уравнений другого, умноженного на какое-либо число. Рассмотрим СЛУ (1). Введем матрицы Тогда система (1) запишется в виде AX=B. Теорема.Если m=n (т.е. число уравнений равно числу неизвестных, т.е. А – квадратная матрица) и Доказательство. Поскольку det A Замечание.Формула (2) дает матричный метод решения систем линейных уравнений. Из формулы (2) можно вывести метод определителей (правило Крамера). Учитывая введение обозначения, равенство (2) запишем более подробно:
Отсюда
Учитывая разложение Пример. Решить систему
матричным методом и методом Крамера. а) найдем определитель системы
Тогда обратная матрица А-1 имеет вид
Значит, решение записывается в виде
Итак, б) ранее нашли
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 436. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
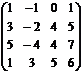
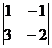 = -2+3=1
= -2+3=1  0. Значит, к
0. Значит, к  2.
2.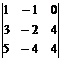 = -8+0-20-0+16+12=0
= -8+0-20-0+16+12=0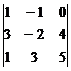 = -10+0-4-0-12+15= -11
= -10+0-4-0-12+15= -11 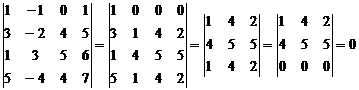 .
. линейно независима, то прибавление к элементу линейной комбинации остальных приводит к линейно независимой системе ) при элементарных преобразованиях строк ранг матрицы не меняется. По этой причине ранг матрицы можно найти с помощью элементарных преобразований строк (или столбцов), приводя матрицу к ступенчатому виду. Число нулевых строк такой матрицы будет равен рангу.
линейно независима, то прибавление к элементу линейной комбинации остальных приводит к линейно независимой системе ) при элементарных преобразованиях строк ранг матрицы не меняется. По этой причине ранг матрицы можно найти с помощью элементарных преобразований строк (или столбцов), приводя матрицу к ступенчатому виду. Число нулевых строк такой матрицы будет равен рангу.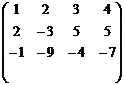 . Прибавим ко второй строке 1-ю, умноженную на (-2), к 3-й строке прибавим 1-ю. Получим
. Прибавим ко второй строке 1-ю, умноженную на (-2), к 3-й строке прибавим 1-ю. Получим 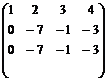 . Вычитая из 3-й строки 2-ю получим
. Вычитая из 3-й строки 2-ю получим 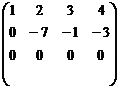 . Значит, ранг равен 2.
. Значит, ранг равен 2.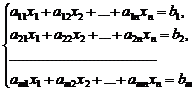 (1)
(1)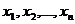 . Можно считать, что коэффициенты aij
. Можно считать, что коэффициенты aij 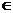 С.
С.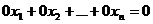 ;
;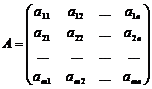 ,
, 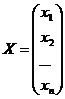 ,
, 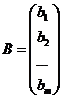 .
.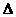 = det A
= det A 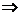 ( А-1A)X= А-1B
( А-1A)X= А-1B  =
= 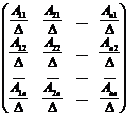
 .
.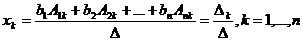 (3).
(3).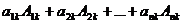 по k-му столбцу замечаем, что
по k-му столбцу замечаем, что 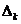 получается заменой k-го столбца определителя
получается заменой k-го столбца определителя 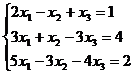
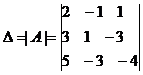 = -8-9+15-5-18-12= -37.
= -8-9+15-5-18-12= -37.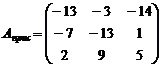 ,
, 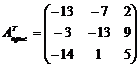 .
.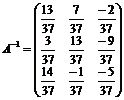 .
.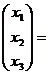
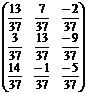
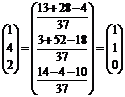 .
.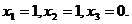
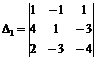 = -4-12+6-2-9-16= -37,
= -4-12+6-2-9-16= -37, 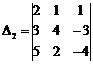 = -32+6-15-20+12+12= -37,
= -32+6-15-20+12+12= -37, 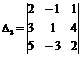 =4-9-20-5+24+6=0.Тогда
=4-9-20-5+24+6=0.Тогда