
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кривые второго порядка. Приведение уравнения кривой второго порядка к каноническому виду. Эллипс. Гипербола. Парабола.В общей декартовой системе координат линия второго порядка может быть задана уравнением ( коэф-ты при произведении переменных и при их первых степенях обозначены 2B,2D и 2E, так как ниже часто будут употребляться половины этих коэф-тов) в котором коэф-ты A,B и C не равны нулю одновременно. Исследуем множество точек, которое ему удовлетворяют, не предполагая заранее, что хоть одна точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид ур-я (1) не изменится. При повороте базиса декартовой прямоугольной системы координат на угол φ старые координаты точки x,y будут связаны с ее новыми координатами x’, y’ формулами (
В новых координатах ур-е (1) примет вид Здесь многоточием обозначены члены первой степени относительно x’ ,y’ и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением x’y’ в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэф-та при x’y’ есть
Если B=0, то переворачивать систему координат не будем. Если , то выберем угол φ так, чтобы B’ обратилось в нуль. Это требование приведет к уравнению 2Bcos2φ=(A-C)sin2φ (2) Если A=C , то cos2φ=0, и можно положить φ=п/4. Если же , то выберем . Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота система координат на этот угол линия будет иметь уравнение 
Выражение для коэф-тов уравнения (3) через коэф-ты (1) подсчитать не трудно, но это не нужно. Теперь коэф-т при произведении переменных равен нулю, а остальные члены мы по- прежнему считаем произвольными. Предложение1. Если в уравнении (3) входят с ненулевым коэф-том квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты. В самом деле, пусть, например, . Перепишем (3) в виде
Если мы сделаем перенос начала координат, определяемый формулами x’’=x’+D’/A’, y’’=y’, то уравнение приведется к виду
Как и требовалось доказать. A. Преположим, что , т.е. оба коэф-та отличны от нуля. Согласно предположению 1 при помощи переноса начала координат уравнение приведется к виду Могут быть сделаны следующие предположения относительно знаков коэф-тов в этом уравнении. A1. - коэф-ты A’ и C’ имеют один знак. Для F’’ имеются следующие три возможности. A1a. Знак F’’ противоположен знаку A’ и C’. Переносим F’’ в другую часть равенства и разделим на него. Уравнение примет вид где Оределение. Линия, которая в некоторой декартовой прямоугольной системе координат может быть заданна уравнением (5) при условии a≥b, называется эллипсом, уравнение называется каноническим уравнениемэллипса, а система координат- его канонической системой координат. При a=b уравнение (5) есть уравнение окружности радиуса a.Таким образом, окружность – частный случай эллипса. A1б. Знак F’’ совпадает с общим знаком A’’ и C’’. Тогда аналогично предыдущему мы можем привести уравнение к виду Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, которое приводится к каноническому виду (7) называется уравнением мнимого эллипса. A1в. F’’=0. Уравнение имеет вид Ему удовлетворяет только одна точка x’’=0, y’’=0/ Уравнение, приводящееся к каноническому виду (8), называется уравнением пары мнимых пересекающихся прямых. Основанием для этого названия служит сходство с приведенным ниже уравнением (10). A2. A’C’<0 – коэф-ты A’ и C’ имеют разные знаки. Относительно F’’ имеются следующие две возможности. A2a.F’’ Определение. Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением (9), называется гиперболой, уравнение называется каноническим уравнениемгиперболы, а система координат – ее канонической системой координат. A2б.F’’=0. Уравнение имеет вид Его левая часть разлагается на множители ax’’-cy’’ и ax’’+cy’’ и, следовательно. Обращается в нуль тогда и только тогда, когда равен нулю хоть один из сомножителей. Поэтому линия с уравнением (10) состоит из двух прямых. Эти прямые пересекаются в начале координат, и мы имеем, таким образом, пару пересекающихся прямых. Б. Допустим теперь, что A’C’=0, и, следовательно, один из коэф-тов A’ или C’ равен нулю. В случае необходимости, делая замену (6), мы можем считать, что A’=0. При этом С
Б1. Пусть D’
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода
или где p=-D’/C’. Мы можем считать, что p>0, т.к. в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: Определение. Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением (11) при условии p>0, называется параболой, уравнение называется каноническим уравнением параболы, а система координат- ее канонической системой координат. Б2. Допустим, что D’=0. Уравнение имеет вид Б2а.C’F’’<0- знаки C’ и F’’- противоположны. Разделив на C’, приведем уравнение к виду Левая часть уравнения разлагается на множители y’’+a и y’’-a. Обращение в нуль каждого из них определяет прямую линию. Эти прямые параллельны, и, таким образом, уравнение определяет пару параллельных прямых. Б2б. С’F’’>0 – знаки C’ и F’’совпадают. Разделив на C’, приведем уравнение к виду Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническое виду (13), называют уравнением пары мнимых параллельных прямых. Б2в. F’’=0. После деления на C’ уравнение принимает вид Это уравнение эквивалентно уравнению y’’=0, и поэтому определяет прямую линию. Уравнение, приводящееся к каноническому виду (14), называется уравнением пары совпавших прямых. Соберем вместе полученные результаты. Теорема1. Пусть в декартовой системе координат задано уравнение второго порядка(1). Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов: 1) 3) 4) 7) В соответствии с этим существует семь классов линий второго порядка Уравнения 2)мнимого эллипса и уравнению 8)пары мнимых параллельных прямых не удовлетворяет ни одна точка. Эллипс. Эллипсом наз-ся линия, которая в прямоугольной декартовой системе координат определяется канонич. уравнением
при условии a≥b>0. Из уравнения (1) следует, что для всех точек эллипса |x|≤a и |y|≤b. Значит эллипс лежит в прямоугольнике со сторонами 2a и 2b. Точки пересечения эллипса с осями канонической системы координат, имеющие координаты (a,0), (-a,0), (0,b), и (0,-b), называются вершинами эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса. Предложение 1.Оси канонической системы координат яв-ся осями симметрии эллипса, а начало канонической системы - его центром симметрии эллипса. Внешний вид эллипса проще всего описать сравнением с окружностью радиуса a с центром в центре эллипса: С эллипсом связаны две замечательные точки, называемые его фокусами. Пусть по определению и c≥0. Фокусами называют точки Для окружности с=0, и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не яв-ся окружностью. Отношение называется эксцентриситетом эллипса. Отметим, что ε<1. Предложение 2. Расстояние от произвольной точки M(x,y), лежащий в эллипсе, до каждого из фокусов яв-ся линейной ф-цией от ее абсциссы x
Док-во. Очевидно,
Учитывая равенство (2), это можно преобразовать к виду
Так как x≤a и ε<1, отсюда следует, что справедливо первое из равенств (4): Предложение3. Для того ,чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса 2a Необходимость условия очевидна: если мы сложим равенства (4) почленно, то увидим, что
Докажем достаточность. Пусть для точки M(x,y) выполнено условие (5), т.е
Возведем обе части равенства в квадрат и приведем подобные члены:
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение (2). Мы приведем к равенству С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнение в канонической системе координат (рис.30) Предложение 4.Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса ε. Докажем это предложение для фокуса
из формулы (4) мы видим теперь, что Обратно, пусть для какой-то точки плоскости
Т.к. ε=с/a, это равенство легко приводиться к виду (6), из которого следует уравнение эллипса. Введем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть Дифференцируем его по x: Подставляя
Теперь мы можем написать уравнение касательной:
Упрощая это уравнение, учтем, что
Предложение 5. Касательная к эллипсу в точке Док-во. Нам надо сравнить углы
Гипербола. Гиперболой мы называли линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением Из этого уравнения видно, что для всех точек гиперболы |x|≥a т.е. все точки гиперболы лежат вне вертикальной полосы ширины 2a(рис.32). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами (a,0) и (-a,0), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух , не связанных между собой частей. Они называются ее ветвями. Числа a и b называют соответственно вещественной и мнимой полуосями гиперболы. В точности так же как и для эллипса док-ся Предложение 6. Для гиперболы оси канонической системы координат яв-ся осями симметрии, а начало канонической системы - центром симметрии. Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде y=kx, поскольку мы уже знаем, что прямая x=0 не пересекает гиперболу. Абсциссы точек пересечения находятся из уравнения
Поэтому если Это позволяет указать координаты точек пересечения (ab/υ, abk/υ) и (-ab/υ, -abk/υ), где обозначено υ=( Определение. Прямые с уравнением y=bx/a и y=-bx/a в канонической системе координат называются асимптотами гиперболы. Запишем уравнения асимптот в виде bx-ay=0 и bx+ay=0. Расстояние от точки M(x,y) до асимптот равны соответственно Если точка M находится на гиперболе, то
Предложение 7.Произведение расстояний от точки гиперболы до асимптот постоянно и равно Предложение 8. Если точка движется по гиперболе так, что ее абсцисса по абсолютной величине неограниченно возрастает, то расстояние от точки до одной из асимптот стремится к нулю. Действительно, хотя бы одно из расстояний Введем число с, положив и с>0. Фокусами гиперболы называются точки Предложение 9. Расстояние от произвольной точки M(x,y) на гиперболе до каждого из фокусов следующим образом зависят от ее абсциссы x:
Предложение 10. Для того чтобы точка M лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2a. Необходимость условия уже доказана. Для док-ва достаточности условия его нужно представить в виде Дальнейшее отличается от док-ва предложения 3 только тем, что нужно воспользоваться равенством (10), а не (2) Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями Предложение 11. Для того чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялась эксцентриситету ε. Уравнение касательной к гиперболе в точке
Предложение 12. Касательная к гиперболе в точке 3. Парабола. Параболой мы называли линию, которая в некоторой декартовой прямоугольной системе координат определяется уравнением
при условии p>0 Из уравнения (15) вытекает, что для всех точек параболы x≥0. Парабола проходит через начало координат. Эта точка называется вершиной параболы. Фокусом параболы называется точка F с координатами (p/2,0) в канонической системе координат. Директрисой параболы называется прямая с уравнением x=-p/2 в канонической системе координат Предложение 13.Расстояние от точки M(x,y), лежащей на параболе, до фокуса равно
Для док-ва вычислим квадрат расстояния от точки M(x,y) до фокуса по координатам этих точек : Отсюда в силу x≥0 следует равенство (16). Заметим, что расстояние от точки M до директрисы равно Отсюда вытекает необходимость следующего условия. Предложение14Для того чтобы точка M лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директриссы этой параболы. Докажем достаточность. Пусть точка M(x,y) одинаково удалена от фокуса и от директрисы параболы: Возведя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы (15).Это заканчивает док-во. Параболе приписывается эксцентриситет ε=1. В силу этого соглашения формула верна и для эллипса, и гиперболы, и для параболы Введем ур-е касательной к параболе в точке, лежащей на ней. Пусть 0. Через точку проходит график ф-ции y=f(x), целиком лежащий на параболе. Для ф-ции f(x) выполнено тождество , дифференцируя которое имеем 2f(x)f’(x)=2p. Подставляя x= Упростим его. Для этого раскроем скобки и вспомним Предложение 15.Касательная к параболе в точке Док-во. Рассмотрим касательную в точке
одобные члены, мы получаем из него уравнение педеляется уравнением Но
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 524. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
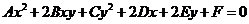 (1)
(1)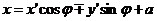 ,
, 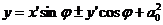 ) ,
) ,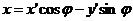 ,
, 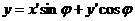 .
.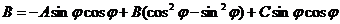 .
.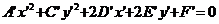 (3)
(3)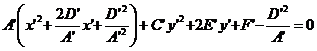
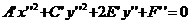 .
.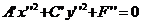 (4)
(4)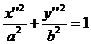 , (5)
, (5)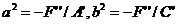 Можно считать, что в этом уравнении a>0,b>0 и a≥b. Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат x*=y’’, y*x’’. (6)
Можно считать, что в этом уравнении a>0,b>0 и a≥b. Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат x*=y’’, y*x’’. (6)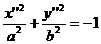 . (7)
. (7)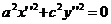 . (8)
. (8) 0. В случае необходимости, делая замену (6), мы можем считать, что знак F’’ противоположен знаку A’. Тогда уравнение приводится к виду
0. В случае необходимости, делая замену (6), мы можем считать, что знак F’’ противоположен знаку A’. Тогда уравнение приводится к виду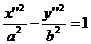 (9) где
(9) где 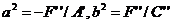 .
.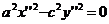 . (10)
. (10)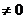 , так как иначе порядок уравнения был бы равен 1, а не 2. Использую предложение 1, мы приведем уравнение к виду
, так как иначе порядок уравнения был бы равен 1, а не 2. Использую предложение 1, мы приведем уравнение к виду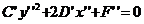
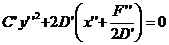 .
.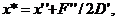
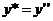 . Тогда уравнение примет вид
. Тогда уравнение примет вид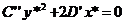
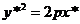 (11)
(11)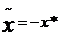 ,
, 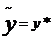 .
.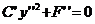 . Относительно F’’ есть следующие три возможности.
. Относительно F’’ есть следующие три возможности.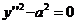 . (12).
. (12).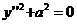 (13)
(13)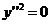 (14)
(14)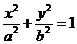 2)
2) 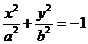
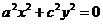
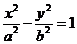 5)
5) 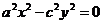 6)
6) 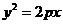
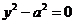 8)
8) 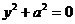 9)
9) 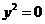
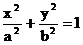 (1)
(1)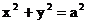 . При каждом x таком, что |x|<a, найдутся две точки эллипса с ординатами
. При каждом x таком, что |x|<a, найдутся две точки эллипса с ординатами 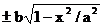 и две точки окружности с ординатами
и две точки окружности с ординатами 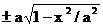 . Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно b/a. Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшается в одном и том же отношении b/a.(рис.28)
. Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно b/a. Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшается в одном и том же отношении b/a.(рис.28)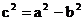 (2)
(2) и
и  с координатами (с,0) и (-с,0) в канонической системе координат(рис.29).
с координатами (с,0) и (-с,0) в канонической системе координат(рис.29).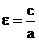 (3)
(3)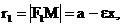
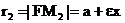 (4).
(4).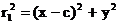 . Подставим сюда выражение для
. Подставим сюда выражение для 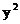 , найденное из уравнения эллипса. Мы получим
, найденное из уравнения эллипса. Мы получим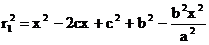 .
.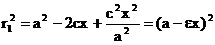
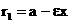 . Второе равенство доказывается аналогично.
. Второе равенство доказывается аналогично.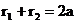 (5)
(5)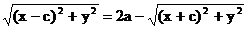 .
.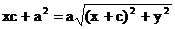 . (6)
. (6)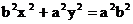 , равносильно уравнению эллипса (1)
, равносильно уравнению эллипса (1)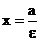 ,
, 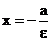 (7)
(7)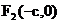 . Пусть M(x,y) - произвольная точка эллипса. Расстояние от M до директрисы с уравнением
. Пусть M(x,y) - произвольная точка эллипса. Расстояние от M до директрисы с уравнением 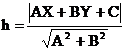 (расстояние от точки до прямой) равно
(расстояние от точки до прямой) равно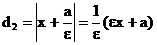
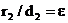
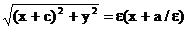 .
.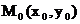 - точка на эллипсе и
- точка на эллипсе и 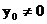 . Через
. Через 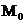 проходит график некоторой ф-ции y=f(x), который целиком лежит на эллипсе. Для нее выполнено тождество
проходит график некоторой ф-ции y=f(x), который целиком лежит на эллипсе. Для нее выполнено тождество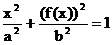 .
.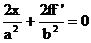
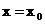 и
и 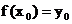 , находим производную от f в точке
, находим производную от f в точке 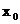 , равную угловому коэф-ту касательной.
, равную угловому коэф-ту касательной.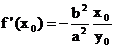
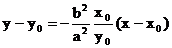 .
.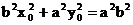 , т.к.
, т.к. 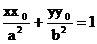 (8)
(8)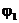 и
и 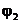 составленные векторами
составленные векторами 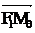 и
и 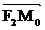 с вектором n, перпендикулярным касательной (рис.31). Из уравнения (8) находим, что n(
с вектором n, перпендикулярным касательной (рис.31). Из уравнения (8) находим, что n( 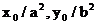 ), и поэтому
), и поэтому Используя (4), мы получаем отсюда, что cos
Используя (4), мы получаем отсюда, что cos 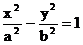 (9)
(9)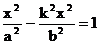 .
.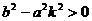 ,то
,то 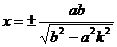
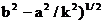 .
.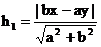 ,
, 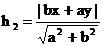
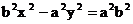 и
и
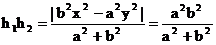
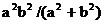 .
. или
или  при этих условиях должно неограниченно возрастать, и, если бы предложение было бы неверно, произведение не было бы постоянно.
при этих условиях должно неограниченно возрастать, и, если бы предложение было бы неверно, произведение не было бы постоянно.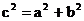 (10)
(10)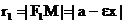 ,
, 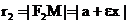 ь (11)
ь (11)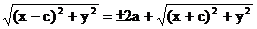
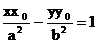 (14)
(14)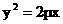 (15)
(15)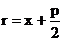 (16)
(16)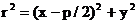 и подставим сюда
и подставим сюда 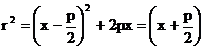 .
.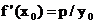 . Теперь мы можем написать уравнение касательной к параболе
. Теперь мы можем написать уравнение касательной к параболе 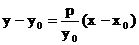
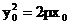 . Теперь уравнение касательной принимает окончательный вид
. Теперь уравнение касательной принимает окончательный вид 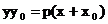 (17)
(17)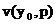 . Значит,
. Значит, 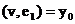 и
и 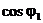 =
= 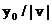 . Вектор
. Вектор 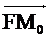 имеет компоненты
имеет компоненты 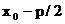 и
и 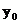 , а потому
, а потому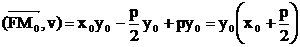 fтавляямеем 2 араболе.к параболе для параболы
fтавляямеем 2 араболе.к параболе для параболы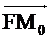 =
= 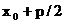 . Следовательно,
. Следовательно, 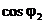 =
=