
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фундаментальная система решений однородных СЛАУ. Общее решение.Пусть Система Применим к системе (2) метод Гаусса. Получим систему ступенчатого вида из rуравнений, где r – ранг матрицы системы (в случае необходимости переобозначаем переменные): Считая
(3)
При фиксированных Лемма.Если Док-во:Пусть AX=0 – матричная запись системы (2). Тогда
Теорема.Фундаментальная система решений (2) содержит (n-r) решений, т.е. размерность пространства решений системы (2) равна числу свободных переменных. Док-во: Построим конкретную фундаментальную систему решений (2). Положим Положим Покажем, что Образуют фундаментальный набор решений системы (2). А) Система Б) Пусть X=
 Итак,
Следствие 1.Совокупность решений системы (2) задается формулой
где r – ранг матрицы системы, n – число неизвестных в системе, Док-во:Любой вектор X, задаваемый формулой (4) является решением системы (2) по лемме. Обратно, любое решение X системы (2) можно записать в виде равенства (4). Это показано при доказательстве предыдущей теоремы. Итак, в формуле (4) содержатся все решения и формула (4) не содержит ничего кроме решений, что и требовалось доказать. Формула (4) называется общим решением системы (2). Задавая конкретные числовые значении, получаем частные решения системы (2). Следствие 2.Общее решение системы (1) задается формулой(если система (1) совместна)
где Док-во: Записывая систему (1) в виде AX=B и подставляя X получим, что Итак , формула (5) содержит все решения системы (1) и не содержит ничего, кроме решений. Значит, формула (5) задает общее решение системы (1). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 629. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1) – некоторая СЛУ
(1) – некоторая СЛУ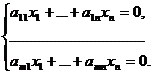 (2) называется однородной СЛУ, соответствующей системе (1). Очевидно, что (0,ююю,0) является решением (2), т.е. система (2) всегда совместна. Значит, система (2) имеет или единственное (называемое нулевым, тривиальным) решение (0,…,0) или имеет бесконечно много решений.
(2) называется однородной СЛУ, соответствующей системе (1). Очевидно, что (0,ююю,0) является решением (2), т.е. система (2) всегда совместна. Значит, система (2) имеет или единственное (называемое нулевым, тривиальным) решение (0,…,0) или имеет бесконечно много решений.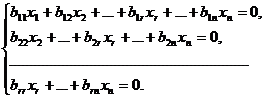
 свободными переменными, получим
свободными переменными, получим
 определяются единственным образом.
определяются единственным образом. решения системы (2), то
решения системы (2), то  является решением системы (2) при
является решением системы (2) при  , т.е. совокупность решений (2) образует линейное пространство.
, т.е. совокупность решений (2) образует линейное пространство. , т.е.
, т.е.  и найдем из (3)
и найдем из (3)  .
. и найдем из (3)
и найдем из (3) 
 и найдем из (3)
и найдем из (3)  .
.
 линейно независима. Действительно, если
линейно независима. Действительно, если  , то такая же зависимость существует между соответствующими координатами. Для (r+1)-x координат получим
, то такая же зависимость существует между соответствующими координатами. Для (r+1)-x координат получим  , т.е.
, т.е.  . Аналогично из зависимостей (r+2)-x,…,n-x координат получим
. Аналогично из зависимостей (r+2)-x,…,n-x координат получим  ,…,
,…,  . Итак,
. Итак,  линейно независимы.
линейно независимы. - произвольное решение системы (2). Рассмотрим
- произвольное решение системы (2). Рассмотрим  . По лемме X’ является решением. По этой же лемме
. По лемме X’ является решением. По этой же лемме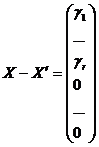 ,где
,где  является решением системы (2). Но, поскольку
является решением системы (2). Но, поскольку  для X-X’, то из (3) получим
для X-X’, то из (3) получим  .
. , т.е. X-X’=0, X=X’, X=
, т.е. X-X’=0, X=X’, X=  . Значит,
. Значит,  (4),
(4),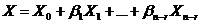 (5)
(5) -какое-либо решение системы (1).
-какое-либо решение системы (1). . Значит формулой (5) определяются решения системы (1). Обратно, если X – произвольное решение системы (1), то
. Значит формулой (5) определяются решения системы (1). Обратно, если X – произвольное решение системы (1), то  -решение системы (2), так как
-решение системы (2), так как  . Значит, по следствию1 найдутся
. Значит, по следствию1 найдутся  такие, что
такие, что  . Отсюда
. Отсюда