
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Смешанного умножения векторовА10. Циклическая перестановка сомножителей не меняет смешанного произведения, т.е. Перестановка двух соседних сомножителей меняет знак смешанного произведения на противоположный, т.е.
Для доказательства достаточно применить доказательство свойства Г20к Чтобы доказать вторую часть свойства, надо воспользоваться определением смешанного произведения и свойством А10 векторного умножения, а затем совершить циклическую перестановку:
А20. Для доказательства этого свойства нужно доказать три равенства:
Докажите их самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов. А30.
Докажите эти равенства самостоятельно, пользуясь определением смешанного произведения и алгебраическими свойствами скалярного и векторного умножения векторов. Замечание. Смешанное произведение
Теорема 1(смешанное произведение в координатах). Если
Применение смешанного произведения Трех векторов Смешанное произведение векторов применяется: 1. Для выяснения компланарности трех векторов: векторы 2. Для вычисления объема параллелепипеда:
3. Для вычисления объема треугольной призмы: 
4. Для вычисления объема тетраэдра (треугольной пирамиды):
Метод координат На плоскости и в пространстве Лекция 7 Аффинная и прямоугольная декартова Системы координат Понятие аффинной и прямоугольной декартовой Систем координат
 , ,  , , 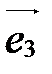 в пространстве, называется аффинной системой координат в пространстве и обозначается в пространстве, называется аффинной системой координат в пространстве и обозначается  или или  (рис. 30). (рис. 30).
ТочкаО называется началом координат, векторы Направленные прямые, на которых положительное направление определяется базисными векторами и которые проходят через точкуО, называются координатными осями:
Оси абсцисс, ординат и аппликат обозначаются и так: Ох, Оу, Оz. Плоскости, определяемые осямиОх и Оу, Оу и Оz, Ох и Оz, называются координатными плоскостями и обозначаются Оху, Оуz, Oxz, а систему координат
 - аффинная система координат, М – произвольная точка пространства. Вектор - аффинная система координат, М – произвольная точка пространства. Вектор  называется радиус-вектором точки М относительно точки О(рис. 32). называется радиус-вектором точки М относительно точки О(рис. 32).
Понятие координат точки вводится на основе понятия координат вектора. Координатами точки М в системе координат Обозначение Если в пространстве задана аффинная система координат, то устанавливается взаимно однозначное соответствие между точками пространства и упорядоченными тройками (х;у;z) действительных чисел. Рассмотрим особенности расположения точки относительно аффинной системы координат, если некоторые ее координаты являются нулевыми. Пусть М(х;у;z). 1) Если z=0, то М(х;у;0)Þ 2) Докажите самостоятельно, что если у=0, то 3) Докажите самостоятельно, что если х=0, то 4) Если z=0 и у=0, то Докажите самостоятельно, что: 5) Если х=0 и у=0, то 6) Если х=0 и z=0, то 7) Так как Чтобы построить точку М(х;у;z) по ее координатам в системе координат
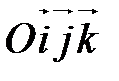 или или 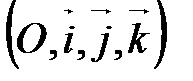 , где , где 
Прямоугольная декартова система координат является частным случаем аффинной. Замечание. На плоскости аффинная система координат состоит из точкиО (начала координат) и двух базисных векторов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 221. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

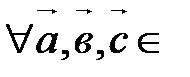 V.
V. ,
,  и к
и к  . Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах
. Параллелепипед будет тот же, только за основание будет принята другая грань (в первом случае – построенная на векторах 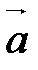 и
и 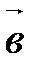 , во втором – на векторах
, во втором – на векторах  и
и  .
.
 .
.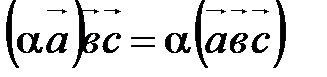 ;
; 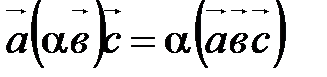 ;
;  .
. ;
; ;
; .
. .
. , т.к.
, т.к.  .
.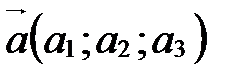 ,
, 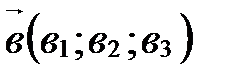 ,
,  в базисе
в базисе 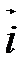 ,
, 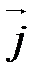 ,
, 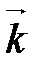 , то
, то  .
.
 .
.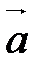 ,
, 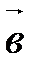 ,
, 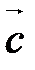 компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда 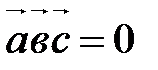 .
. (рис. 27).
(рис. 27). (рис. 28).
(рис. 28). (рис. 29).
(рис. 29).

 ,
,  , - координатными векторами:
, - координатными векторами:  - ось абсцисс;
- ось абсцисс; - ось ординат;
- ось ординат; - ось аппликат (рис. 31).
- ось аппликат (рис. 31). или просто М(х;у;z): х – абсцисса точки М, у – ордината, z– аппликата.
или просто М(х;у;z): х – абсцисса точки М, у – ордината, z– аппликата. Þ
Þ  . Верно и обратное:
. Верно и обратное:  , и наоборот, если
, и наоборот, если  , и наоборот, если
, и наоборот, если  и
и  Þ
Þ  . Верно и обратное:
. Верно и обратное:  и наоборот, если
и наоборот, если  , то х=0 и у=0.
, то х=0 и у=0. и наоборот, если
и наоборот, если  , то из пунктов 1) – 3) следует, чтоО(0;0;0) в системе координат
, то из пунктов 1) – 3) следует, чтоО(0;0;0) в системе координат 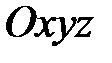 .
.

 ,
,  ,
,  и
и  .
. . Прямоугольная декартова система координат на плоскости изображена на рис. 35.
. Прямоугольная декартова система координат на плоскости изображена на рис. 35.
