
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства координат векторов10. Нулевой вектор в любом базисе имеет нулевые координаты: □ Разложим
Следовательно, 20. Если □
30. Если
в базисе □ По определению координат вектора
Тогда Сложим почленно эти равенства и воспользуемся свойствами сложения векторов и умножения вектора на число:
По определению координат вектора
Из свойства 30 получаем следствия: Следствие 1. Каждая координата суммы (разности) двух векторов равна сумме (разности) соответствующих координат этих векторов. Следствие 2. При умножении вектора на число каждая его координата умножается на это число. □ Чтобы доказать справедливость следствия 1, надо в свойстве 30 взять сначала a=b=1, а затем a=1, b=-1. Для доказательства следствия 2 полагаем b=0. ■ 40. Векторы равны тогда и только тогда, когда равны их соответствующие координаты: 50. Пусть
Пусть
Если же
Частным случаем произвольного базиса является ортонормированный базис. Его удобно использовать при решении метрических задач (т.е. задач, связанных с вычислением длин отрезков (векторов) и величин углов).
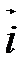 , , 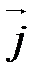 , , 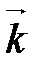 называется ортонормированным, если его векторы удовлетворяют двум условиям: называется ортонормированным, если его векторы удовлетворяют двум условиям: 1)
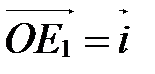 , ,  , , 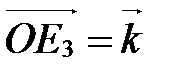 (рис. 8), то углы (рис. 8), то углы  , ,  и и  - прямые. - прямые.
Замечание. Множество всех векторов, параллельных данной плоскости (или лежащих в ней), образует двумерное векторное пространство, т.к. любой его базис состоит из двух неколлинеарных векторов. Поэтому любой вектор этого пространства в таком базисе имеет две, а не три координаты:
Лекция 4 Нелинейные операции над векторами Скалярное произведение двух векторов
Углом между ненулевыми векторами
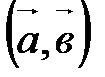 . .
Два ненулевых вектора Обозначение: Если хотя бы один из векторов нулевой, то считают, что Итак, нулевой вектор ортогонален любому вектору. Угол между двумя векторами
Понятие угла между векторами используется при определении понятия скалярного произведения. Скалярным произведениемдвух векторов называется число (скаляр), равное произведению их длин на косинус угла между ними. Обозначение:
Скалярным квадратом вектора Скалярное умножение векторов не является линейной операцией над векторами. Скалярное умножение векторов обладает геометрическими и алгебраическими свойствами. В геометрических свойствах фигурируют геометрические величины (длина, угол, перпендикулярность, проекция и т.д.), алгебраические свойства – это свойства, аналогичные свойствам сложения и умножения действительных чисел. Геометрические свойства |
|||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 229. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (0;0;0).
(0;0;0). по векторам базиса
по векторам базиса  ,
,  ,
, 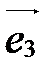 :
: .
. (1;0;0),
(1;0;0), 
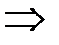


 (
(  ;
;  ;
;  ),
),  в базисе
в базисе  , то
, то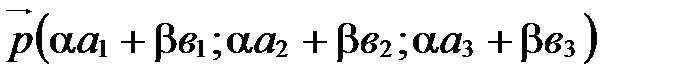
 ,
,  .
. ,
,  .
.
 .
.
 . ■
. ■

 ,
, 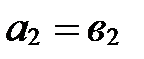 ,
,  .
.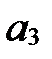 ),
),  ,
,  и
и  , i=1, 2, 3. Векторы
, i=1, 2, 3. Векторы  коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны:
коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны: .
.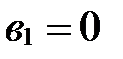 . Тогда
. Тогда и
и  .
. , то
, то , а
, а  - любые.
- любые.

 ;
; . Ортонормированный базис выглядит так:
. Ортонормированный базис выглядит так: 
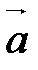 и
и 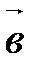 называется угол между лучами
называется угол между лучами  и
и  , сонаправленными с векторами
, сонаправленными с векторами 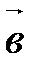
 .
. .
.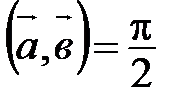 .
. .
. или
или  .
. .
. . Обозначение:
. Обозначение: