
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторное произведение двух векторовПусть 1) длина 2) 3) базис
На рис. 20 изображены векторные произведения Геометрические свойства Векторного умножения векторов Г10. Пусть или
или Пусть
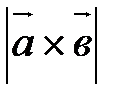 векторного произведения векторов векторного произведения векторов 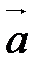 и и 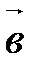 равна площади параллелограмма, построенного на этих векторах. равна площади параллелограмма, построенного на этих векторах.
По определению
Следовательно,
Алгебраические свойства Векторного умножения векторов А10. А20. А30. Замечание. Пользуясь определениями ортонормированного базиса и векторного произведения двух векторов, можно доказать, что
Попробуйте доказать самостоятельно! Теорема 1 (векторное произведение в координатах). Если
По определению координат вектора в базисе
Тогда
(получите это равенство, проделав все выкладки самостоятельно). Применение векторного произведения Векторное произведение двух векторов применяется: 1. Для выяснения коллинеарности двух векторов: 
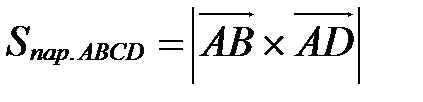 (рис. 21). (рис. 21).
3. Для вычисления площади треугольника: Лекция 6 Нелинейные операции над векторами Смешанное произведение трех векторов
Смешанным или скалярно-векторным произведением трех векторов, взятых в указанном порядке, называется скалярное произведение первого вектора на векторное произведение второго и третьего. Обозначение: Таким образом, по определению
Смешанное произведение – это число! Геометрические свойства Смешанного умножения векторов Г10. Пусть
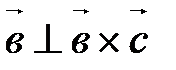 и и 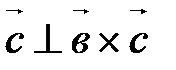 . .
Следовательно, векторы Обратно, пусть векторы
т.е. Г20 (геометрический смысл модуля смешанного произведения). Если векторы Пусть векторы
Построим на векторах Пусть n – луч, перпендикулярный основанию параллелепипеда и лежащий в том же полупространстве, что и вектор
а) Если тройка Итак, б) Если тройка Итак, Из пунктов а) и б) следует, что Алгебраические свойства |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 218. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
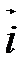 ,
, 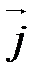 ,
, 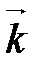 - ортонормированный базис трехмерного векторного пространства V (правый). Векторным произведением двух неколлинеарных векторов
- ортонормированный базис трехмерного векторного пространства V (правый). Векторным произведением двух неколлинеарных векторов 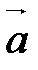 и
и 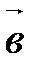 называется вектор, обозначаемый
называется вектор, обозначаемый 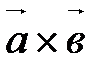 (или
(или 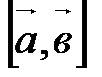 ) и удовлетворяющий трем условиям:
) и удовлетворяющий трем условиям: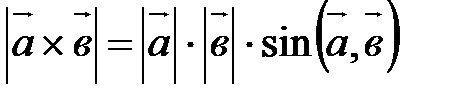 ;
;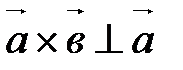 и
и 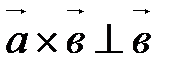 ;
;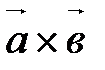
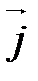
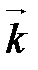
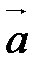
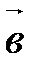
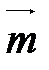
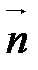
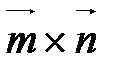
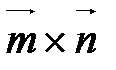 .
.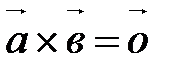

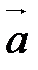 ||
|| 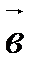 .
.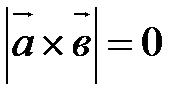
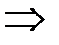
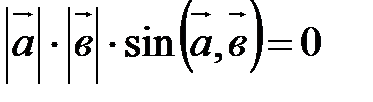
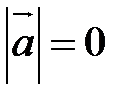
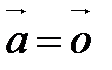
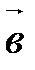 ;
;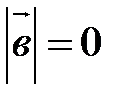
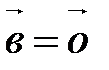
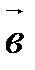 ||
|| 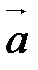
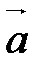 ||
|| 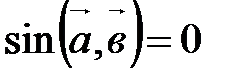
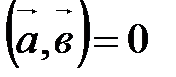 или
или 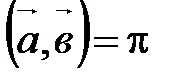
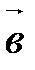
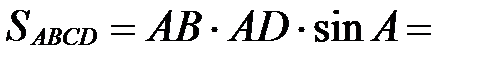
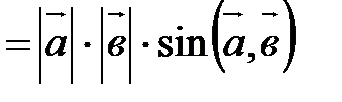 (рис. 20).
(рис. 20).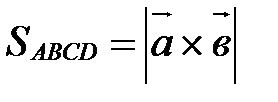 .
.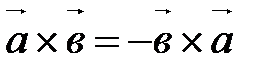
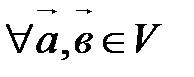 .
.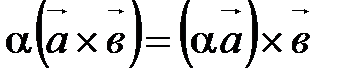
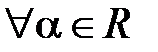 .
.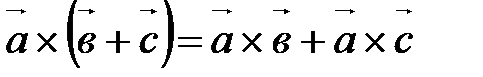
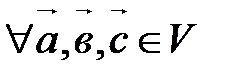 .
.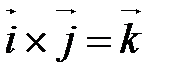 ;
;
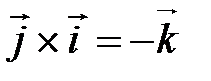 ;
;
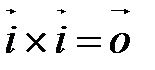 ;
;
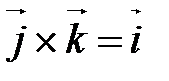 ;
;
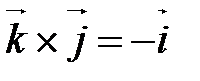 ;
;
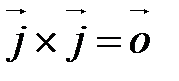 ;
;
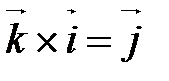 ;
;
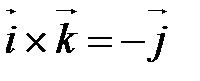 ;
;
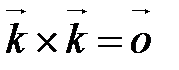 .
.
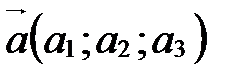 ,
, 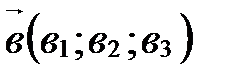 в базисе
в базисе 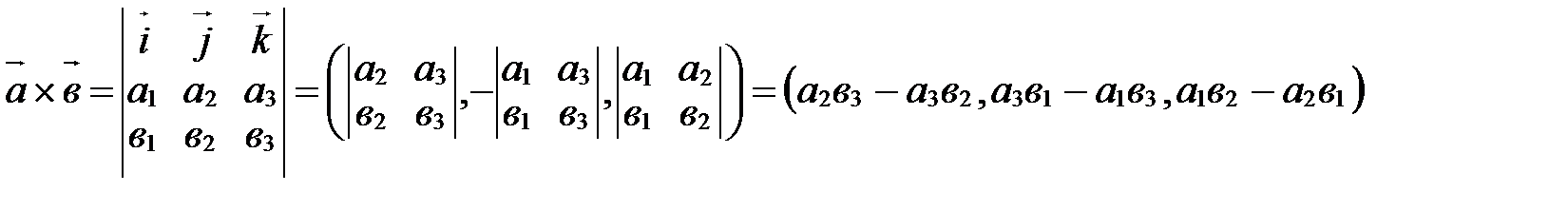 .
.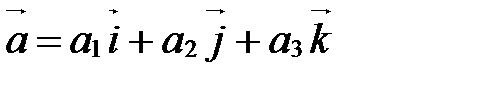 ,
, 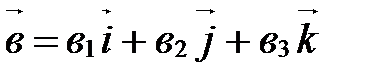 .
.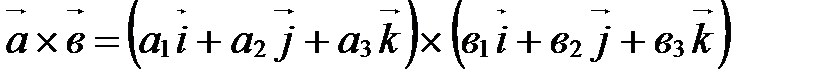 . Используя свойства А10-А30 векторного умножения и замечание, получим:
. Используя свойства А10-А30 векторного умножения и замечание, получим: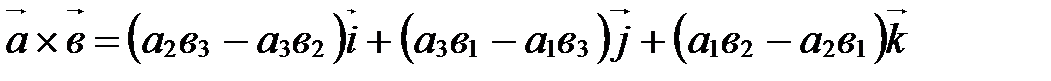
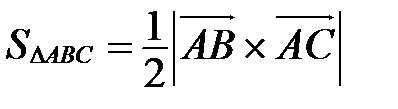 .
.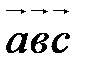 .
.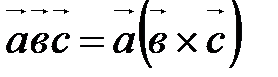 .
.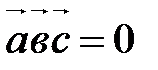
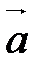 ,
, 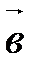 ,
, 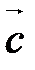 компланарны.
компланарны.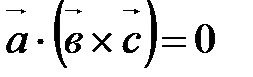
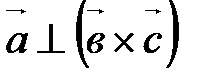 .
.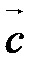
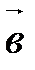
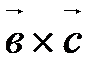
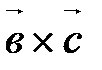 (рис. 24),т.е. векторы
(рис. 24),т.е. векторы  , которой они параллельны.
, которой они параллельны.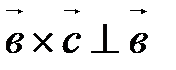 ,
, 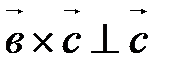 Þ
Þ 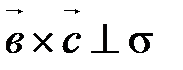 , а так как
, а так как 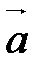 ||
|| 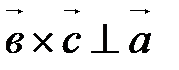 Þ
Þ 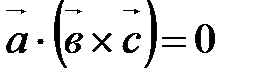 ,
,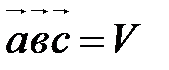 , если тройка
, если тройка 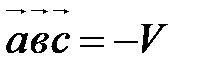 , если тройка
, если тройка 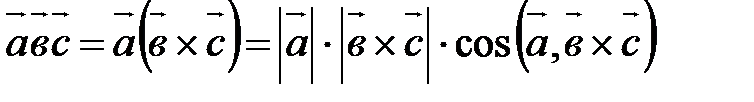 . Пусть
. Пусть 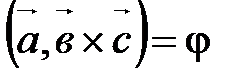 .
.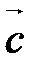
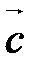
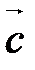
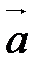
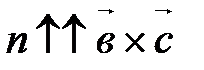 (рис. 26, а) Þ
(рис. 26, а) Þ 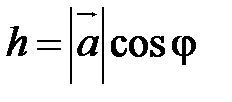 ÞÞ
ÞÞ 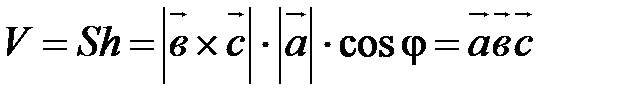 .
.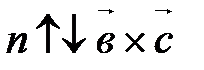 (рис. 26, б) Þ
(рис. 26, б) Þ 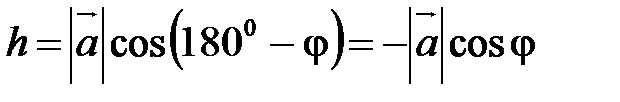 ÞÞ
ÞÞ 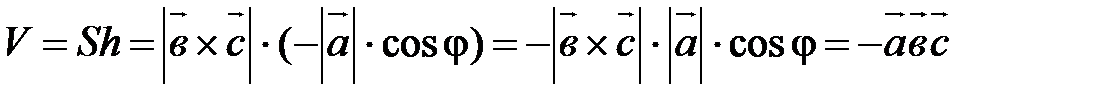 .
.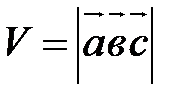 .
.