
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Скалярного умножения векторовГ10. □ Пусть или
или Обратно, пусть Г20. Скалярный квадрат вектора равен квадрату его длины: □ Из этого свойства получаем важное следствие:
Прежде чем сформулировать третье свойство, дадим понятие проекции вектора Пусть даны два вектора Возьмем в пространстве произвольную точкуА и отложим от нее вектор
Возьмем прямуюs|| Проекцией (скалярной) вектора
Обозначение: Г30. Алгебраические свойства Скалярного умножения векторов А10. А20. А30. Следствие. Теорема 1 (скалярное произведение в координатах). Если в ортонормированном базисе
□ По определению координат вектора
Следствие 1. Следствие 2 (условие ортогональности двух векторов в координатах).
Следствие 3.
 по перемещению материальной точки из положения по перемещению материальной точки из положения  в положение в положение  (рис. 12): (рис. 12):
Лекция 5 Нелинейные операции над векторами Понятие об ориентации пространства и плоскости 
Пусть
 , ,  , , 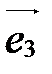 называется правым (левым), если при взгляде на плоскость векторов называется правым (левым), если при взгляде на плоскость векторов  и и  из конца третьего вектора из конца третьего вектора 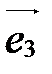 кратчайший поворот от первого вектора кратчайший поворот от первого вектора  ко второму вектору ко второму вектору  виден как идущий против часовой стрелки (по часовой стрелке). На рис. 16 изображен правый базис, на рис. 17 – левый. виден как идущий против часовой стрелки (по часовой стрелке). На рис. 16 изображен правый базис, на рис. 17 – левый.
Можно дать и другие определения правого и левого базиса, например, такое: базис Мы будем пользоваться в дальнейшем первым определением. Если два базиса правые (или левые), то говорят, что они одинаково ориентированы или имеют одинаковую ориентацию. Если один базис правый, а другой – левый, то говорят, что они противоположно ориентированы или имеют противоположную ориентацию. Множество всех правых (всех левых) базисов в пространстве V называется правой (левой) ориентацией векторного пространства V. Таким образом, в векторном пространстве ориентацию можно задать двумя способами: правую и левую. Векторное пространство, в котором выбрана ориентация, называется ориентированным. Как только в пространстве мы зададим базис, так сразу оно становится ориентированным. В дальнейшем, если нет специальных оговорок, когда в пространстве выбран базис, будем считать, что он является правым. Аналогично можно ввести понятие ориентированной плоскости. При этом базис |
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 243. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 .
.
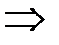
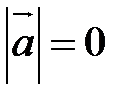
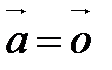
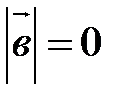
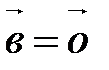



 . ■
. ■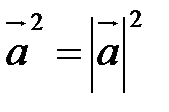 .
. .■
.■ .
.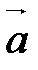 на направление, определяемое вектором
на направление, определяемое вектором 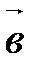 .
. (рис. 11).
(рис. 11).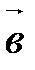

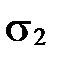
 , через точку В – плоскость
, через точку В – плоскость  . Пусть
. Пусть  ,
,  .
. на направление, определяемое вектором
на направление, определяемое вектором  , называется число, равное
, называется число, равное , если
, если  ;
; , если
, если  .
. .
. .
.
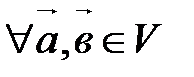 .
. ;
; 
 .
.
 .
. . Это свойство можно распространить и на большее число слагаемых.
. Это свойство можно распространить и на большее число слагаемых.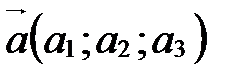 ,
, 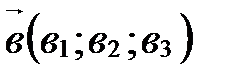 , то
, то .
. ,
,  . Используя свойства Г10,Г20, А10-А30 и то, что
. Используя свойства Г10,Г20, А10-А30 и то, что  ,
,  ,
,  и
и  , получаем:
, получаем:
 . ■
. ■ .
.
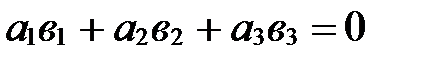 .
. .
.
 .
.
