
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ)Вариант № 5
Часть 1 1.Бегун пробежал 250 м за 36 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
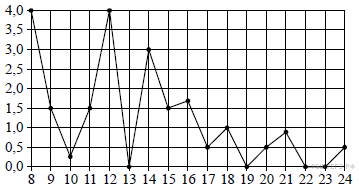
Ответ: 25 509187 25 Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад. 2.На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа в Томске впервые выпало ровно 1,5 миллиметра осадков.
Ответ: 9 509828 9 Источник: ЕГЭ — 2015. Досрочная волна, вариант А. Ларина. 3.
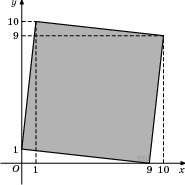
Найдите площадь квадрата, вершины которого имеют координаты (9; 0), (10; 9), (1; 10), (0; 1).
Ответ: 82 21347 82 4.За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом. 
Ответ: 0,25 325904 0,25 5.Найдите корень уравнения: Ответ: 0,3 77384 0,3 6.
Ответ: 3,5 509193 3,5 Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад. 7.На рисунке изображён график функции y = f(x) и шесть точек на оси абсцисс: x1, x2, x3, …, x6. В скольких из этих точек производная функции f(x) положительна?
Ответ: 2 509151 2 Источник: СтатГрад: Диагностическая работа по математике 13.02.2015 вариант МА00410. 8.Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
Часть 2
Ответ: 54 76439 54 Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1. 9.Найдите значение выражения Ответ: 25 26845 25 10.Груз массой 0,38 кг колеблется на пружине. Его скорость v меняюется по закону
Ответ: 0,76 513958 0,76 11.Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Ответ: 65 113655 65 12.Найдите наименьшее значение функции
Ответ: 2 315635 2 13. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2017. Задания С1., Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 3. (Часть C). 14.Дан правильный тетраэдр MABC с ребром 1. Найдите расстояние между прямыми AL и MO, где L — середина ребра MC, O — центр грани ABC.
Источник: МИОО: Тренировочная работа по математике 10.02.2011 вариант 2. (Часть С) 15.Решите неравенство
16.К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3? Источник: Задания 16 (С4) ЕГЭ 2015 17. В августе 2020 года взяли кредит. Условия возврата таковы: — каждый год долг увеличивается на r%; — с февраля по июль необходимо выплатить часть долга. Кредит можно выплатить за четыре года равными платежами по 777 600 рублей, или за два года равными платежами по 1 317 600 рублей. Найдите r.
Источник: Задания 17 (С5) ЕГЭ 2017 18.Найдите все значения a, при каждом из которых наибольшее значение функции
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016 19.Моток веревки режут без остатка на куски длиной не меньше 115 см, но не больше 120 см (назовем такие куски стандартными). а) Некоторый моток веревки разрезали на 23 стандартных куска, среди которых есть куски разной длины. На какое наибольшее число стандартных одинаковых кусков можно было бы разрезать тот же моток веревки? б) Найдите такое наименьшее число
|
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 534. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

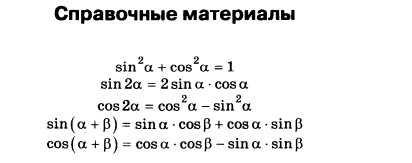
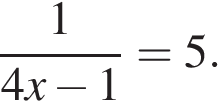
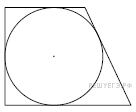 Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.
Периметр прямоугольной трапеции, описанной около окружности, равен 32, её большая боковая сторона равна 9. Найдите радиус окружности.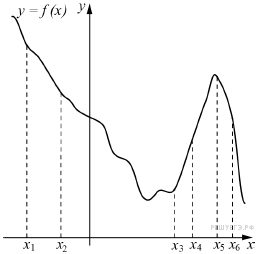
 , а высота равна 3.
, а высота равна 3.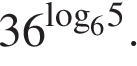
 где
где  — время с момента начала колебаний, T = 2 с — период колебаний,
— время с момента начала колебаний, T = 2 с — период колебаний, 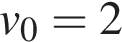 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле 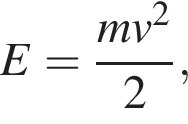 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 57 секунд после начала колебаний. Ответ дайте в джоулях.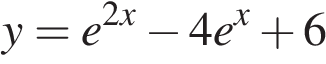 на отрезке
на отрезке 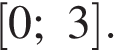
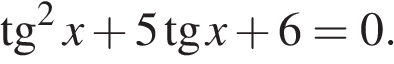
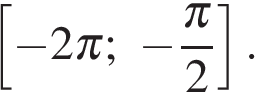
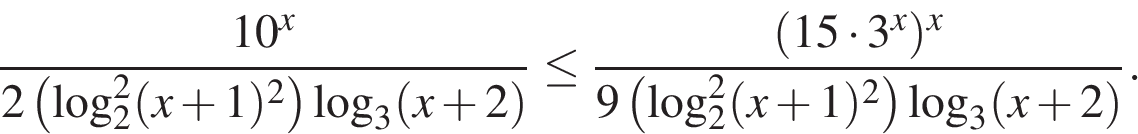
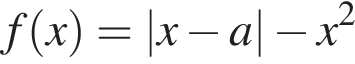 не меньше 1.
не меньше 1.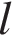 , что любой моток веревки, длина которого больше
, что любой моток веревки, длина которого больше