
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ)Вариант № 3
Часть 1 1.В доме, в котором живёт Игорь, один подъезд. На каждом этаже по шесть квартир. Игорь живёт в квартире 69. На каком этаже живёт Игорь?
Ответ: 12 502984 12 Источник: МИОО: Тренировочная работа по математике 14.11.2013 вариант МА10201. 2.На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало не менее 3 миллиметров осадков.
Ответ: 3 513416 3 Источник: СтатГрад: Тренировочная работа по математике 03.03.2016 вариант МА10409 3.
Ответ: 10 27552 10 4.Маша включает телевизор. Телевизор включается на случайном канале. В это время по трем каналам из тридцати показывают телевикторины. Найдите вероятность того, что Маша попадет на канал, где телевикторины не идут.  Ответ: 0,9 1007 0,9 5.Найдите корень уравнения:
Ответ: -3 11149 -3 6.
Ответ: 48 27605 48 7.
Ответ: -0,5 510403 -0,5 Источник: МИОО: Тренировочная работа по математике 22.04.2014 вариант МА10602. 8.
Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
Часть 2
Ответ: 27 27081 27 9.Найдите значение выражения
Ответ: 15 66703 15 10.Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой
Ответ: 500 54799 500 11.Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Ответ: 27 99568 27 12.Найдите наибольшее значение функции
Ответ: 5 282862 5 13.а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г. 14.Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка M — середина бокового ребра пирамиды AP. 15.Решите неравенство
Источник: Задания 15 (С3) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 301 (C часть). 16.В трапеции АBCD угол BAD прямой. Окружность, построенная на большем основании АD как на диаметре, пересекает меньшее основание BC в точке C и M. а) Докажите, что угол BАM равен углу CАD. б) Диагонали трапеции АBCD пересекаются в точке O. Найдите площадь треугольника АOB, если АB = 6, а BC = 4BM.
Источник: Задания 16 (С4) ЕГЭ 2017 17.31 декабря 2014 года Валерий взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определённое количество процентов), затем Валерий переводит очередной транш. Валерий выплатил кредит за два транша, переводя в первый раз 660 тыс рублей, во второй — 484 тыс. рублей. Под какой процент банк выдал кредит Валерию?
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко. 2015 г. 18.Найдите все значения a, для каждого из которых уравнение
Источник: СтатГрад: Тренировочная работа 21.04.2017 вариант МА10709 19.Имеется 8 карточек. На них записывают по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают. а) Может ли в результате получиться 0? б) Может ли в результате получиться 1? в) Какое наименьшее целое неотрицательное число может в результате получиться? |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 587. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если уравнение имеет более одного корня, в ответе укажите меньший из них. 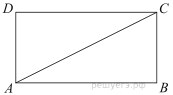 Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

 , где
, где  — температура нагревателя (в градусах Кельвина),
— температура нагревателя (в градусах Кельвина),  — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя
— температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя  , если температура холодильника
, если температура холодильника  К? Ответ выразите в градусах Кельвина.
К? Ответ выразите в градусах Кельвина.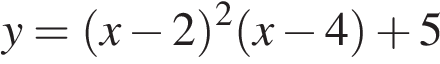 на отрезке
на отрезке 



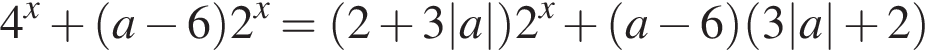 имеет единственное решение.
имеет единственное решение.