
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ)Стр 1 из 12Следующая ⇒ ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ) Вариант № 1
Часть 1 1.На бензоколонке один литр бензина стоит 35 руб. 60 коп. Водитель залил в бак 15 литров бензина и купил бутылку воды за 23 рубля. Сколько рублей сдачи он получит с 1000 рублей? Решение.
Пятнадцать литров бензина стоят 534 руб., водитель потратил 534 + 23 = 557 руб., поэтому он получит 443 руб. сдачи.
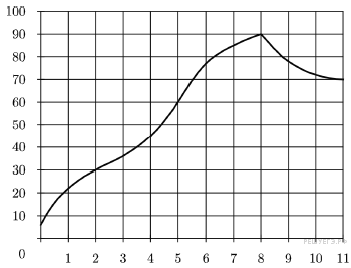
Ответ: 443. Ответ: 443 323833 443 Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2. 2.На графике показано изменение температуры двигателя в процессе разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат — температура двигателя в градусах Цельсия. Определите по графику, на сколько градусов нагреется двигатель со второй по пятую минуту разогрева.
Решение. Из графика видно, что значение температуры двигателя на вторую минуту нагрева равно 30°C, а на пятую — 60°C. Следовательно, двигатель нагрелся на 30°C.
Ответ: 30. Ответ: 30 507896 30 Источник: СтатГрад: Диагностическая работа по математике 21.01.2015 вариант МА10110. 3.
 Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Ответ: 6. Ответ: 6 246703 6 4.В сборнике билетов по истории всего 60 билетов, в 18 из них встречается вопрос по теме "Смутное время". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Смутное время". Решение. Из 60 билетов 42 не содержат вопроса по теме "Смутное время", поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме "Смутное время", равна
Ответ: 0,7. Ответ: 0,7 286335 0,7 5.Найдите корень уравнения:
Решение. Избавимся от знаменателя:
Ответ: −6. Ответ: -6 10153 -6 6.
Решение. Рассмотри угол AOB в треугольнике AOB:
Ответ: 119. Ответ: 119 27764 119
7. Решение.Отрицательным значениям производной соответствуют интервалы, на которых функция
Ответ:5. Ответ: 5 317739 5 8.Вершина A куба
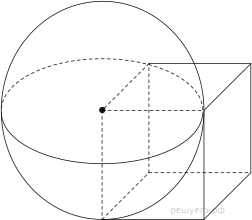
Часть 2 Решение. Так как ребро куба равно радиусу сферы, в кубе содержится 1/8 часть сферы и, соответственно, 1/8 ее поверхности, равная
Ответ: 1,28. Ответ: 1,28 27206 1,28 9.Найдите значение выражения Решение. Выполним преобразования:
Ответ: 11. Ответ: 11 26973 11 10.Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: Решение. Найдем, в какой момент времени после начала работы температура станет равной
Через 4 минуты после включения прибор нагреется до 1650 К, и при дальнейшем нагревании может испортиться. Таким образом, прибор нужно выключить через 4 минуты.
Ответ: 4. Ответ: 4 28113 4 11. Первые 140 км автомобиль ехал со скоростью 50 км/ч, следующие 160 км — со скоростью 60 км/ч, а затем 120 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.Решение.Чтобы найти среднюю скорость на протяжении пути, нужно весь путь разделить на все время движения. Средняя скорость автомобиля равна:
Ответ: 63. Ответ: 63 513342 63 Источник: СтатГрад: Тренировочная работа по математике 20.01.2016 вариант МА10309 12.Найдите наибольшее значение функции
Решение. Найдем производную заданной функции:
Ответ: 5. Ответ: 5 3457 5 13.а) Решите уравнение б) Укажите корни данного уравнения, принадлежащие промежутку Решение. а) Имеем:
б) Из найденных решений промежутку
Ответ: а) Критерии проверки: 14.В пирамиде DABC прямые, содержащие ребра DA и BC, перпендикулярны. а) Постройте сечение плоскостью, проходящей через точку E — середину ребра DB, и параллельно DA и BC. Докажите, что получившееся сечение является прямоугольником. б) Найдите угол между диагоналями этого прямоугольника, если DA = 30, BC = 16. Решение.
а) Построение Значит б)
Заметим, что
Ответ: Критерии проверки: Источник: Пробный экзамен по математике Кировского района Санкт-Петербурга, 2015. Вариант 2. 15.Решите неравенство: Имеем:
Рассмотрим два случая. Первый случай:
Второй случай:
Таким образом, множество решений данного уравнения:
Приведём другое решение. Заметим, что
Воспользуемся методом рационализации:
Ответ: Критерии проверки: 16.Дана окружность радиуса 6 с центром в точке О, расположенной на биссектрисе угла, равного Пусть Q — центр искомой окружности радиуса х, М — точка касания с данной окружностью, В — точка касания с одной из сторон данного угла с вершиной А. Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому
Линия центров касающихся окружностей проходит через точку их касания, поэтому Пусть точка О лежит между А и Q (рис. 2),
тогда
Ответ: 3 или 21. Критерии проверки: 17. В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи y кг никеля в день требуется y2 человеко-часов труда. Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором 1 кг алюминия приходится на 2 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод? Решение. Пусть в первой области х рабочих заняты на добыче алюминия, а 50 − х рабочих заняты на добыче никеля, и пусть во второй области y рабочих заняты на добыче алюминия, а 50 − y рабочих заняты на добыче никеля. Внесем данные из условия в таблицу.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C). 18.Найдите все значения параметра a, при каждом из которых система уравнений
имеет ровно два решения. Решение. Первое уравнение системы раскладывается на множители: (x − 2y)(y − 2x) = 0. Следовательно, уравнение задаёт пару прямых x = 2y и y = 2x. Второе уравнение при каждом a ≠ 0 — уравнение окружности c центром (a, a) и радиусом Если Пусть Можно воспользоваться геометрическим методом или использовать формулу расстояния от точки до прямой.
Отсюда a = ± 0,2.
Ответ: a = ± 0,2.
Комментарий: на самом деле, конечно, задача сводится к исследований количества решений системы
То есть, уравнения
При Критерии проверки: Источник: СтатГрад: Тренировочная работа по математике 22.04.2015 вариант МА10409. 19.За победу в шахматной партии начисляют 1 очко, за ничью — 0,5 очка, за проигрыш — 0 очков. В турнире принимают участие m мальчиков и d девочек, причём каждый играет с каждым дважды. а) Каково наибольшее количество очков, которое в сумме могли набрать девочки, если m = 2, d = 2? б) Какова сумма набранных всеми участниками очков, если m + d = 10? в) Каковы все возможные значения d, если и известно, что в сумме мальчики набрали ровно в 3 раза больше очков, чем девочки?
ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ) Вариант № 2
Часть 1 1.Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за три шоколадки, покупатель получает четыре (одну в подарок). Сколько шоколадок можно получить на 290 рублей в воскресенье? Решение. Разделим 290 на 35:
Значит, можно будет купить 8 шоколадок. Еще 2 будут даны в подарок. Всего можно будет получить 10 шоколадок.
Ответ: 10. Ответ: 10 507895 10 Источник: СтатГрад: Диагностическая работа по математике 21.01.2015 вариант МА10110. 2.На рисунке жирным точками показан курс доллара, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали − цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольший курс доллара за указанный период. Ответ дайте в рублях.
Решение. Из рисунка видно, что наибольший курс доллара был установлен 22 сентября и составил 31,1 рубля.
Ответ: 31,1. Ответ: 31,1 500884 31,1 3. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому см2.
Ответ: 14. Ответ: 14 5191 14 4.В сборнике билетов по химии всего 50 билетов, в 16 из них встречается вопрос по углеводородам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам. Решение. Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по углеводородам, равна
Ответ: 0,32. Ответ: 0,32 501746 0,32 Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402. 5.Найдите корень уравнения Решение. Последовательно получаем:
Ответ: −15. Ответ: -15 518950 -15 Источник: СтатГрад: Тренировочная работа 21.12.2017 вариант МА10210 6.В параллелограмме ABCD AB = 3, AD = 21, Решение. Большая высота проведена к меньшей стороне. Имеем:
Ответ: 18. Ответ: 18 27436 18 7.На рисунке изображен график производной функции
Решение. Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых ее производная неотрицательна, то есть промежуткам (−6; −5,2] и [2; 6). Данные промежутки содержат целые точки 2, 3, 4 и 5. Их сумма равна 14.
Ответ: 14. Ответ: 14 6429 14 8.
Часть 2 Решение. Диагональ квадрата, лежащего в основании призмы, является диаметром описанного вокруг призмы цилиндра. Тогда объем цилиндра:
Ответ: 4. Ответ: 4 27050 4 9.Найдите значение выражения: Решение. Используем формулу синуса двойного угла :
Ответ: 18. Ответ: 18 17289 18 10.Расстояние от наблюдателя, находящегося на высоте Решение. Задача сводится к решению уравнений и при заданном значении :
Следовательно, чтобы видеть горизонт на более далеком расстоянии, наблюдателю нужно подняться на 151,25 − 11,25 = 140 метров. Для этого ему необходимо подняться на 140 : 0,2 = 700 ступенек.
Ответ: 700. Ответ: 700 42665 700 11.Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч. Решение. Скорость сближения поездов равна 60 км/ч или 1 км/мин. Следовательно, за 1 минуту 3 секунды пассажирский поезд сместится относительно товарного на 1,05 км. При этом он преодолеет расстояние, равное сумме длин поездов. Поэтому длина пассажирского поезда равна 1050 − 900 = 150 м.
Ответ: 150. Ответ: 150 517235 150 Источник: СтатГрад: Тренировочная работа 21.04.2017 вариант МА10710 12.Найдите точку максимума функции
Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: 10. Ответ: 10 4063 10 13.а) Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку Решение. а) Запишем исходное уравнение в виде: Значит, или что невозможно, или откуда или б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:
Ответ: а) б) Критерии проверки: Источник: Задания 13 (С1) ЕГЭ 2015 14.Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна Решение.
Пусть — середина ребра — середина ребра По теореме о средней линии треугольника следовательно, точки лежат в одной плоскости. следовательно, точки являются вершинами параллелограмма. Кроме того, а по теореме о трёх перпендикулярах, так как получим поэтому этот параллелограмм — прямоугольник. Значит, искомое расстояние есть длина отрезка Отрезок равен По теореме Пифагора
Ответ: Критерии проверки: 15.Решите неравенство Решение. Решение будем искать при условиях:
Рассмотрим исходное неравенство на множестве тогда откуда то есть Рассмотрим исходное неравенство на множестве тогда откуда то есть или
Ответ: Критерии проверки: 16.В треугольнике ABC AB = 13, BC = 10, CA = 7. Точка D лежит на прямой BC так, что BD : DC = 1 : 4. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF. Решение. Пусть AD = d, BD = x, DC = y. Возможны два случая. Первый случай. Точка D лежит на отрезке BC (верхний рисунок):
Значит, Второй случай. Точка D лежит вне отрезка BC (нижний рисунок):
Значит,
Ответ: 6 или 8. Критерии проверки: Источник: МИОО: Диагностическая работа по математике 20.10.2010 вариант 4. (Часть С) 17.15 января планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его возврата таковы: − Первого числа месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r целое число. − Со 2 по 14 число необходимо выплатить часть долга. − 15 числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей
Найдите наибольшее r, при котором сумма выплат будет меньше 1,25 млн руб. Решение. Долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
Пусть тогда долг на первое число каждого месяца равен:
Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:
Общая сумма выплат составляет:
По условию, общая сумма выплат будет меньше 1,25 млн рублей, значит,
Наибольшее целое решение этого неравенства — число 9. Значит, искомое число процентов — 9.
Ответ: 9%. Критерии проверки: Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 412. Запад (C часть). 18. Найдите все значения а, при каждом из которых система
не имеет решений. Решение. Рассмотрим второе неравенство системы
Если , то неравенство, а значит, и система не имеет решений. Если , то решение неравенства — луч
Если , то решение неравенства — луч
При первое неравенство системы принимает вид
Если , то решение этой системы — два луча с концами в точках Если , то решение этой системы — полуинтервал с концами в точках
Отметим, что точки нет во множестве решений первого неравенства. Очевидно, что при , решение системы будет содержать луч, вида , где большее из чисел и , а значит система будет иметь решение. Для того, чтобы система не имела решений, при необходимо и достаточно:
Учитывая случай , получаем ответ.
Ответ: Критерии проверки: Источник: МИОО: Диагностическая работа по математике 19.11.2009 с решениями: вариант 2. (Часть С) 19.Ученики одной школы писали тест. Результатом каждого участника является целое неотрицательное число баллов. Ученик считается сдавшим тест, если он набрал не менее 83 баллов. Из-за того, что задания оказались слишком трудными, было принято решение всем участникам теста добавить по 5 баллов, благодаря чему количество сдавших тест увеличилось. а) Могло ли оказаться так, что после этого средний балл учеников, не сдавших тест, понизился? б) Могло ли оказаться так, что после этого средний балл учеников, сдавших тест, понизился, и средний балл учеников, не сдавших тест, тоже понизился? в) Известно, что первоначально средний балл участников теста составил 90, средний балл учеников, сдавших тест, составил 100, а средний балл учеников, не сдавших тест, составил 75. После добавления баллов средний балл учеников, сдавших тест, стал равен 103, а не сдавших — 79. При каком наименьшем числе участников теста возможна такая ситуация?
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 534. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

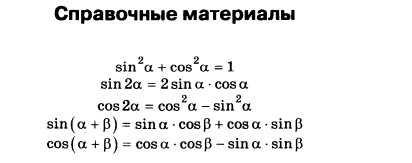
 Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах. см2.
см2.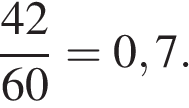


 В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
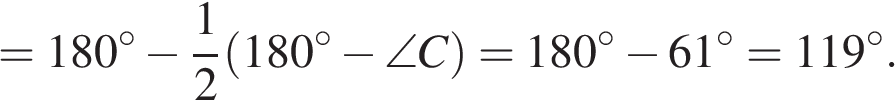
 На рисунке изображён график функции
На рисунке изображён график функции 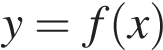 и двенадцать точек на оси абсцисс:
и двенадцать точек на оси абсцисс:  ,
,  ,
,  ,
,  ,
,  В скольких из этих точек производная функции
В скольких из этих точек производная функции  отрицательна?
отрицательна? Таких точек 5.
Таких точек 5. с ребром 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину
с ребром 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину 



 , где t — время в минутах,
, где t — время в минутах, 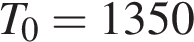 К,
К,  К/мин
К/мин  ,
,  К/мин. Известно, что при температуре нагревателя свыше 1650 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
К/мин. Известно, что при температуре нагревателя свыше 1650 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах. К. Задача сводится к решению уравнения
К. Задача сводится к решению уравнения  при заданных значениях параметров a и b:
при заданных значениях параметров a и b:

 на отрезке
на отрезке 
 Уравнение
Уравнение  не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является
не имеет решений, производная положительна при всех значениях переменной, поэтому заданная функция является возрастающей. Следовательно, наибольшим значением функции на заданном отрезке является
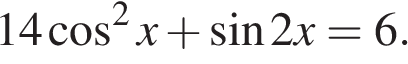
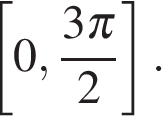


 принадлежат числа
принадлежат числа  ,
,  и
и 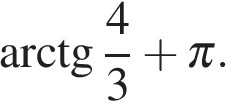

 б)
б) 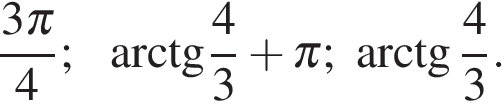

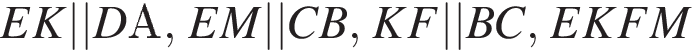 — искомое сечение, параллелограмм
— искомое сечение, параллелограмм 
 — прямоугольник.
— прямоугольник. и
и  — середина
— середина  тогда
тогда  — средняя линия треугольника
— средняя линия треугольника  значит,
значит,  аналогично
аналогично 
 так как
так как  Пусть
Пусть  пересекает
пересекает  в точке
в точке 

 Применим теорему косинусов в треугольнике
Применим теорему косинусов в треугольнике 
 следовательно,
следовательно, 

 Решение.
Решение.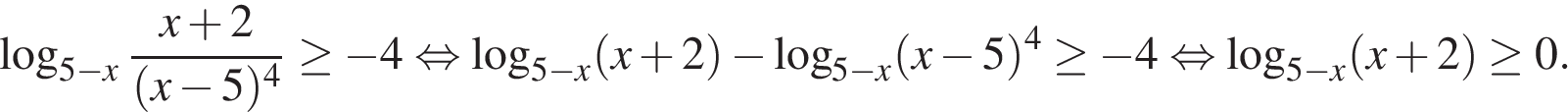



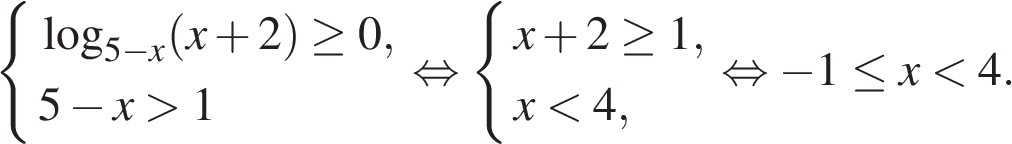



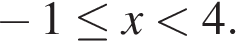
 Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 15.Решение.
Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки О до вершины угла равно 15.Решение. Из прямоугольного треугольника BAQ находим, что
Из прямоугольного треугольника BAQ находим, что  Пусть точка Q лежит между А и О (рис. 1).
Пусть точка Q лежит между А и О (рис. 1).
 , или
, или  , откуда находим, что
, откуда находим, что 

 , или
, или  , откуда
, откуда 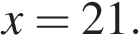


 то система имеет единственное решение и поэтому не удовлетворяет условию задачи.
то система имеет единственное решение и поэтому не удовлетворяет условию задачи. Тогда условие задачи выполнено тогда и только тогда, когда окружность касается каждой из прямых. То есть расстояние от центра до каждой из прямых равно радиусу окружности.
Тогда условие задачи выполнено тогда и только тогда, когда окружность касается каждой из прямых. То есть расстояние от центра до каждой из прямых равно радиусу окружности.

 которое имеет единственное решение при
которое имеет единственное решение при
 прямые пересекаются, поэтому исходная система имеет не два, а всего одно решение.
прямые пересекаются, поэтому исходная система имеет не два, а всего одно решение.
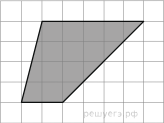 Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
 . Найдите большую высоту параллелограмма.
. Найдите большую высоту параллелограмма. 
 , определенной на интервале
, определенной на интервале  Найдите промежутки возрастания функции
Найдите промежутки возрастания функции 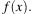 В ответе укажите сумму целых точек, входящих в эти промежутки.
В ответе укажите сумму целых точек, входящих в эти промежутки.
 В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы.
. Найдите объем цилиндра, описанного около этой призмы. ,если cos
,если cos 
 м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле
м над землeй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле  , где
, где  км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 12 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 44 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 12 км. К пляжу ведeт лестница, каждая ступенька которой имеет высоту 20 см. На какое наименьшее количество ступенек нужно подняться человеку, чтобы он увидел горизонт на расстоянии не менее 44 километров?
 Искомая точка максимума
Искомая точка максимума

 , высота равна
, высота равна  Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно
Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно
