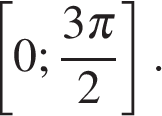Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПРОБНЫЙ ЭКЗАМЕН ЕГЭ-2018 МАТЕМАТИКА (ПРОФИЛЬ)Вариант № 8
Часть 1 1. В квартире установлен прибор учёта расхода холодной воды (счётчик). Показания счётчика 1 января составляли 121 куб. м воды, а 1 февраля — 131 куб. м. Сколько нужно заплатить за холодную воду за январь, если стоимость 1 куб. м холодной воды составляет 13 руб. 50 коп.? Ответ дайте в рублях. Ответ: 135 517147 135 Источник: ЕГЭ по математике 31.03.2017. Досрочная волна. 2.На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.
Ответ: 6 26874 6 3.
Ответ: 4,5 324464 4,5 4.Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.  Ответ: 0,16 509191 0,16 Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад. 5.Найдите корень уравнения:
Ответ: -5 11649 -5 6.
В треугольнике
Ответ: 0,28 27342 0,28 7.Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.Ответ: 0,125
119972 0,125 8.
Часть 2Ответ: 1,25 72353 1,25 9.Найдите значение выражения Ответ: 9 61845 9 10.Груз массой 0,25 кг колеблется на пружине. Его скорость v меняется по закону Ответ: 0,16 513893 0,16 11.Смешали некоторое количество 13-процентного раствора некоторого вещества с таким же количеством 15-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора? Ответ: 14 108689 14 12.Найдите наименьшее значение функции
Ответ: -6 512499 -6 Источник: СтатГрад: Тренировочная работа по математике 18.12.2015 вариант МА10211. 13.а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку 14.Отрезок AC ― диаметр основания конуса, отрезок AP ― образующая этого конуса и AP = AC . Хорда основания BC составляет с прямой AC угол 60°. Через AP проведено сечение конуса плоскостью, параллельной прямой BC. Найдите расстояние от центра основания конуса O до плоскости сечения, если радиус основания конуса равен 1. Источник: Пробный экзамен по математике Санкт-Петербург 2014. Вариант 1. 15.Решите неравенство
Источник: МИОО: Тренировочная работа по математике 12.04.2011 вариант 1. (Часть С) 16.На диагонали параллелограмма взяли точку, отличную от её середины. Из неё на все стороны параллелограмма (или их продолжения) опустили перпендикуляры. а) Докажите, что четырёхугольник, образованный основаниями этих перпендикуляров, является трапецией. б) Найдите площадь полученной трапеции, если площадь параллелограмма равна 16, а один из его углов равен 60°.
Источник: МИОО: Тренировочная работа по математике 22.04.2014 вариант МА10601. 17.15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина. 18.Найдите все значения a, для каждого из которых существует хотя бы одна пара чисел x и y, удовлетворяющих неравенству
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 701. 19.Каждый из 32 студентов писал или одну из двух контрольных работ, или написал обе контрольные работы. За каждую работу можно было получить целое число баллов от 0 до 20 включительно. По каждой из двух контрольных работ в отдельности средний балл составил 14. Затем каждый студент назвал наивысший из своих баллов (если студент писал одну работу, то он назвал балл за неё). Среднее арифметическое названных баллов равно S. а) Приведите пример, когда S < 14. б) Могло ли оказаться, что только два студента написали обе контрольные работы, если S = 11? в) Какое наименьшее количество студентов могло написать обе контрольные работы, если S = 11? |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 428. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.

 угол
угол  равен 90°, высота
равен 90°, высота  равна 24,
равна 24, 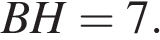 Найдите
Найдите 
 Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
 где t — время с момента начала колебаний, T = 16 с — период колебаний,
где t — время с момента начала колебаний, T = 16 с — период колебаний,  м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле
м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле 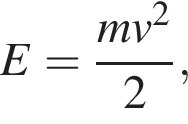 где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 2 секунды после начала колебаний. Ответ дайте в джоулях.
где m — масса груза в килограммах, v — скорость груза в м/с. Найдите кинетическую энергию груза через 2 секунды после начала колебаний. Ответ дайте в джоулях.