
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение весомости показателей.Определяется функция, нормализующая весомость i-го показателя в ранжируемой последовательности ϕ(i). ϕ0(i) = ϕ̅ (i)/ ∑i-1n ϕ̅ (i) (5) При недостаточности исходных данных можно считать, что весомость разных показателей одинакова ⇒ КТУ = Для определения весомости показателей используется метод экспертных оценок, при которых экспертам предлагается перечень показателей для указания их весомости или в долях единицы или по 10-балльной шкале. Допустим, что экспертами при разработке УАБ малой дальности, предназн. для поражения прочных целей проведена экспертная оценка значимости показателей, которые сведены в таблице 1:
Таблица 1.
T= Tприменения /2n tϕ(i) = tавт. навигация и управления / tполет.УАБ Обработка мнений экспертов проводится на основании ⇒формул математической статистики: = ∑i-1 nϕ(i)j / m (7 ϕ̅ (i)), где ϕ̅ (i) – среднее арифметическое весомости i-го показателя ϕ(i)j – весомость i-го показателя, указанная j-м экспертом m – число экспертов Ϭ̅(i) = √∑j-1m (ϕ(i)j - ϕ(i))2/m (8), где Ϭ̅(i) – средне-квадратичное отклонение (СКО) для i-го показателя V(i) = Ϭ̅(i)×100/ φ́(i) (9), где V(i) – коэффициент изменчивости мнения экспертов по i-му показателю - показатель вариаций Si= ∑i-1n ρi(10), где  ρi– ранг оценки весомости i-го показателя Si– сумма рангов по i-ому показателю S̅ = ∑i-1nSi/ n (11) S̅ - среднее арифметическое значение суммы рангов по всем n показателей di= Si–S(12) di–отклонение суммы рангов от средн. арифметического значения Ti= ∑t=1Li (t3li – tli) (13) Ti– показатель связности рангов L – количество групп связанных рангов tli – количество связанных рангов в l-ой группе по i-му показателю ω = 12×∑i-1ndi2 / m2(n3-1) – m∑i-1nTi(14) ω – коэффициент конкордации, характеризующий согласованность мнений экспертов по всем n показателям χφ2= 12×∑i-1ndi2 / m× n(n+1) – ∑i-1nTi ×1/(n-1) (15) χφ2 – фактическое значение критерия (хи-квадрат) Распределение χφ2 дает возможность оценить степень согласованности теоретического χ2 и фактического распределения χφ2юДалее определяются значения: ϕ̅ (i), ϕ0(i), Ϭ̅(i),V(i) по формулам (7), (5), (8), (9).
Таблица 2.
Рассмотреть подсчет рангов для каждого показателя: Расчет рангов весомостей оценочных показателей
Талица 3. В таблице 3 показан подсчёт рангов весомостей для показателей,указанных экспертами .В левом верхнем углу квадрата вписаны весомости для каждого показателя,взятого из табл 2 если в ранжированной последовательности весомостей по данному показателю несколько эксперементов показали одинаковые значения,то ранг для данной весомости определяется как среднее значение из натуральн. ряда чисел. Если жевесомость в ранжиров. Последовательности встречается только одинраз, то её ранг понижается , следуя к числу натурального ряда. Например для первого показателя ( Среднее арифметическое значение сумм ранга Отклонение суммы ранга от среднего арифметического значения равны:
Коэффициент конкордации , которыйхарактеризует согласованность мнений экспертов по всем показателям: W=152,4/3672=0,0415 Если w=1 ,то мнения полностью совпадают Если w=-1, то мнения противоположны Так как w>0,то можно считать ,что мнения экспертов согласованы. Если установить уровень значимости в 5%,то при числе показателей n=5, число степеней свободы ν=n-1=4, и табличное значение
P- вероятность того , что критерий
Фактическое значение :
Табличное значение:
Вывод:Фактическое значение > табличного , что говорит так же о достаточной согласованности мнений экспертов по всей совокупности характеристик. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 350. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 /n(6)
/n(6)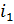 ) весомость =1 встречается двараза,следовательно , ранг этой весомости =1+2/2.
) весомость =1 встречается двараза,следовательно , ранг этой весомости =1+2/2. :
: 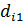 =15-13.4=1.6;
=15-13.4=1.6;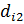 =14-13.4=0.6 ;
=14-13.4=0.6 ;  =.-1.9;
=.-1.9;  =1.6;
=1.6;  =-1.9
=-1.9
 =(
=(  +(
+(  =(
=(  =(
=(  +(
+(  =(
=(  =(
=(  =108
=108 зависит от числа степеней свободы ν и вероятности P(=0,95 т.к. 5%)
зависит от числа степеней свободы ν и вероятности P(=0,95 т.к. 5%) ν, P)
ν, P)