
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Статистическое описание СТС на основе кластерного анализаВ практической деятельности проектирования СТС часто бывает необходимо анализировать и сравнивать довольно большое число альтернативных вариантов. Актуальный при выполнении сравнений альтернативных вариантов является задание их разбиение на отдельные классы (кластеры) и нахождение обобщённого образа, т.е. непосредственных средних характеристик для любого класса. Подобного рода задачи решаются методами кластерного анализа. Чтобы произвести разбиение на классы, вводится понятие близости объекта. Близкие объекты входят в один класс. Мер близости (сходства) оцениваются различными критериями. Функции меры сходства:
Наиболее распространённый критерий – метрический, являющийся функцией расстояния между объектами, представляемыми точками в многомерном пространстве признаков объектов. Рассмотрим вопросы формализованного описания объекта.
Математическое описание объекта – математическая модель, которая отражает основные свойства этого объекта. В общем случае, в качества объектов моделирования выступают как технические средства, так и условия их функционирования.
В задачах проектирования наиболее распространенной формой описания является матрица вида:
Строки матрицы – технические устройства, столбцы – отдельные параметры этих устройств. Аналогично, при описании условий функционирования строки матрицы – некоторые характерное условие функционирования, (целевые задачи, подлежащие выполнению), а столбцы – это признаки (свойства этих условий или целевых задач). Сущность математического описания объекта состоит в выборе совокупности признаков. Важно, чтобы признаки всесторонне отражали объект с точки зрения поставленной задачи.  Симметричная особенность определяющих признаков – их разнородность и несопоставимость, поэтому возникает необходимость нормализации признаков, т.е. приведения их к единой шкале безразмерных оценок свойств объекта. Нормализованные значения признаков могут представлены в виде:
где
Информационные признаки объекта неравноценны. В связи с этим, возникает необходимость введения коэффициентов, которые разделили бы признаки по их важности. Эти весовые коэффициенты отражают приоритеты признаков в проводимом исследовании. Когда известно ранжирование признаков в порядке убывания по их важности, коэффициенты важности могут быть получены по следующей формуле:
где
С учетом нормирования и ранжирования признаков, исходная матрицы
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 327. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
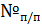
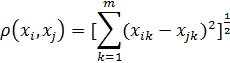
 норма
норма
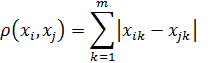
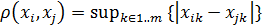
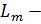 норма
норма
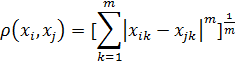
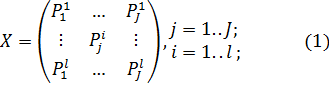

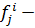 нормализующее значение оценки -го свойства
нормализующее значение оценки -го свойства 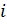 -го объекта;
-го объекта;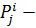 количественное значение оценки -го свойства
количественное значение оценки -го свойства 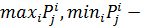 максимальное и минимальное количественное значение -го свойства из всего исходного множества объектов.
максимальное и минимальное количественное значение -го свойства из всего исходного множества объектов.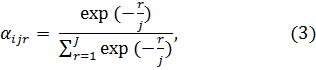
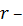 порядковый номер
порядковый номер 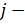 го признака в ранговом ряду.
го признака в ранговом ряду.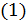 преобразуется к виду:
преобразуется к виду: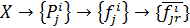
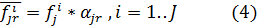
 нормировованый признак с учетом коэффициента важности.
нормировованый признак с учетом коэффициента важности.