
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Подходы к решению задач параметрического синтезаСинтез бывает: - Структурный - Параметрический Целью структурного синтеза является определение рациональной структуры построения СТС, то есть типа подсистем, их состава и компоновки. Задача структурного синтеза выполняется методом перебора структурных схем СТС на дискретном множестве альтернатив задаваемой морфологической матрицей (М:признаков) и/или графиком. Параметрический синтез заключается в оптимальном определении выбора конструкторских параметров и ТТХ основных подсистем при фиксированной структурной схеме СТС. Рассмотрим два основных подхода к решению задачи параметрического синтеза СТС с заданной структурной схемой. Первый подход заключается в последовательном решении задач выбора рационального облика подсистем, входящих в состав СТС, а затем решении задач рационального облика СТС в целом, то есть процесс проектирования направленного «снизу-вверх». Метод решения, используемый здесь – последовательный анализ вариантов. Во втором подходе процесс проектирования направлен «сверху-вниз» от СТС в целом и ее подсистем. Метод решения, используемый здесь – синтез СТС на основе последовательного усложнения модели. Синтез СТС по методу последовательного анализа вариантов Рассмотрим задачу параметрического синтеза СТС при заданной структуре и условиях ее применения. Задача синтеза формализуется так:
Где

Для решения задачи (1) целесообразно использовать 2х-уровневую систему моделей. На 1 уровне находятся модели формирования облика отдельных подсистем СТС, задаваемых соотношениями
Где На 2 уровне расположения операционной модели и модели затрат, которые описывают функционирование системы в целом.
Главным свойством показателей затрат или выделения ресурсов его аддитивный характер. Суть предлагаемого метода синтеза заключается в следующем: 1) Для любой из подсистем назначаются частные показатели эффективности.
В качестве этих показателей Если используются свертки, то индекс Далее составляется ЦФ:
при условии, что при этом
Естественно, что вектор оптимального значения конструкции каждой Т.о. предположение о том, что функционалы
Глобальные критерии эффективности СТС в целом (см.1) оптимизируются на П.(7). При этом:
Т.о. в результате решения задачи (8) производится оптимизация решения по всем подсистемам для заданного на дискретном множестве значений вектора
где при этом По окончательным значениям Т.о. процесс проектирования с использование данного подхода направлен снизу- вверх и включает следующие операции: Полученные для любой подсистемы множества П, зависят от выделенного ресурса который задавался на допустимом дискретном множестве для любой подсистемы. 2) проводится поиск оптимального вектора конструкторских параметров системы в целом по глобальному критерию на множествах оптимальных по П решений для любой подсистемы. Проектирование СТС на основе последовательного усложнения модели Процесс проектирования при данном подходе направлен сверху в низ, от системы в целом к ее подсистеме. Суть метода состоит в следующим: Вектор оптимизированных переменных
Тогда задача 1 принимает вид:
Решение задачи (10) упрощается по сравнению с (1) таким образом, разность В ходе решений задачи(10) получаем условное оптимальности решения для вектора существующих параметров
И ТТХ подсистемы Значение 1]
2]
Где,
Где, Шаг 1. Разделение вектора
При первоначальном выполнении
ξ – заданные точности получения выходных параметров. Если не выполняется хотя бы один из составных номеров, количество итераций увеличивается на 1. Лекция № ??? (дд.мм.гг) (№5 Казаков) |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 464. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
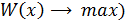 (1)
(1)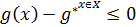
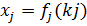
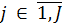
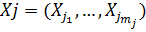
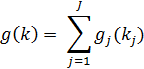
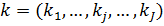
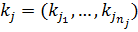
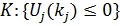
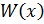 – операционная модель оценки эффективности СТС
– операционная модель оценки эффективности СТС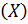 – выбор ТТХ системы в целом размерности m,
– выбор ТТХ системы в целом размерности m, 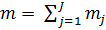
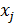 – выбор ТТХ j-ой подсистемы СТС размерности
– выбор ТТХ j-ой подсистемы СТС размерности 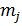
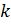 = выбор конструкторских параметров СТС размерности
= выбор конструкторских параметров СТС размерности 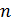 ,
, 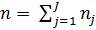
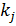 – выбор конструкторских параметров j-ой подсистемы размерности uj
– выбор конструкторских параметров j-ой подсистемы размерности uj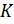 – множество дополнительных конструкторских решений, определяемых возможностями реализации и задаваемые ограничениями
– множество дополнительных конструкторских решений, определяемых возможностями реализации и задаваемые ограничениями 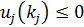
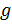 - показатель затрат или выделенных ресурсов для СТС в целом
- показатель затрат или выделенных ресурсов для СТС в целом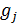 - показатель затрат или выделения ресурсов для j-ой подсистемы СТС
- показатель затрат или выделения ресурсов для j-ой подсистемы СТС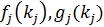 - модели определения вариантов ТТХ подсистем
- модели определения вариантов ТТХ подсистем 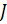 – Общее количество подсистем
– Общее количество подсистем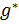 - устанавливаемое в ТТЗ ограничение на показатели затрат или выделяемых ресурсов для СТС
- устанавливаемое в ТТЗ ограничение на показатели затрат или выделяемых ресурсов для СТС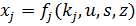 (2)
(2)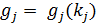
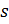 – выбор, определяющий структуру СТС
– выбор, определяющий структуру СТС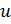 – выбор, описывающий управление и поведение системы в процессе функционирования
– выбор, описывающий управление и поведение системы в процессе функционирования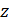 – выбор условий применения СТС
– выбор условий применения СТС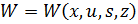
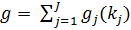 (3)
(3)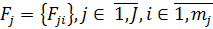
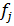 могут использоваться непосредственно ТТХ подсистем
могут использоваться непосредственно ТТХ подсистем 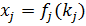 или свертки из показателей, входящих в ТТХ
или свертки из показателей, входящих в ТТХ 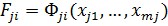
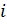 меняется в диапазоне
меняется в диапазоне 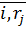 , где
, где 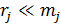
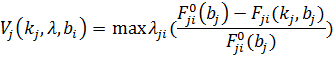
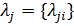
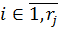
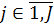 (4)
(4)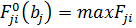 , при
, при 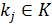

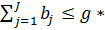 (5)
(5)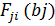 являются функцией выделения ресурса
являются функцией выделения ресурса 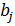 для
для 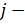 той подсистемы. При фиксированном векторе концентрации
той подсистемы. При фиксированном векторе концентрации 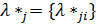 оптимальным является вектор
оптимальным является вектор 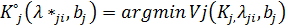 , при
, при 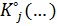 является эффективной альтернативой на множестве ЦФ
является эффективной альтернативой на множестве ЦФ  , и его значения зависят от выделенного ресурса
, и его значения зависят от выделенного ресурса 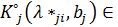 множетству Патеро, подстроенному на функциональный
множетству Патеро, подстроенному на функциональный 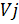 . Само множество Парето для
. Само множество Парето для 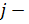 подсистемы зависит от параметров
подсистемы зависит от параметров 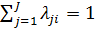 и значения выделенного рес.
и значения выделенного рес. 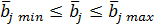 (т.е.
(т.е. 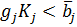 ), и определяя для этих значений точки
), и определяя для этих значений точки 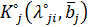 , удовлетворяющие условиям (5) и (6), мы получим все множества Парето для
, удовлетворяющие условиям (5) и (6), мы получим все множества Парето для 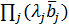 .
.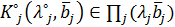 .
.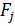 достаточно полно характеризуют облик
достаточно полно характеризуют облик 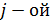 подсистемы приводит к тому, что облик СТС в целом следует искать среди точек Парестровых множеств
подсистемы приводит к тому, что облик СТС в целом следует искать среди точек Парестровых множеств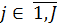 ,
, 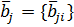 ,
, 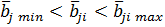 (7)
(7)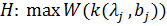
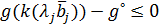
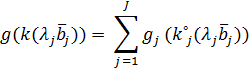
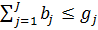 (8)
(8)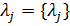 ,
, 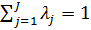 и выбор оптимальных значений .
и выбор оптимальных значений .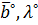 .
. 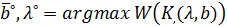 ,
,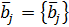 ,
,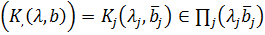 ,
,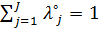 ,
, 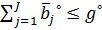
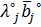 , из множества П, для любой из подсистем оптимизации вектора констант параметров
, из множества П, для любой из подсистем оптимизации вектора констант параметров  ,
, 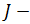 ой локальной задачи оптимизации по частным критериям при суммарно задаваемых на дискретном множестве значениях ресурсов, выделяемых любой подсистеме системой. В результате для любой подсистемы определяется области П, расчет значений вектора концентрации
ой локальной задачи оптимизации по частным критериям при суммарно задаваемых на дискретном множестве значениях ресурсов, выделяемых любой подсистеме системой. В результате для любой подсистемы определяется области П, расчет значений вектора концентрации 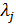 и ограничений на допустимые ресурсы
и ограничений на допустимые ресурсы 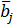 .
.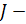 подсистемам.
подсистемам.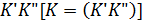 .
.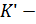 вектор существования параметров, а его компоненты -
вектор существования параметров, а его компоненты - 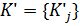 существующие параметры
существующие параметры 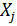 и назначение ресурса выделенного любой подсистеме
и назначение ресурса выделенного любой подсистеме 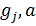 следовательно, на критерий W системы в целом.
следовательно, на критерий W системы в целом. 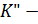 вектор вторичных параметров полагается зарезервированным в контур интерации при решении задачи 1.
вектор вторичных параметров полагается зарезервированным в контур интерации при решении задачи 1.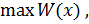
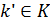
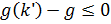
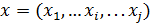
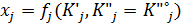
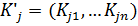
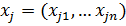
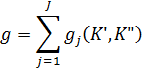
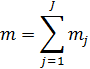
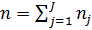 (10)
(10)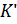 существенно меньшей размерности вектора
существенно меньшей размерности вектора 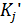 , а так же для занчений ресурса
, а так же для занчений ресурса 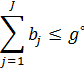
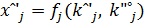 .
.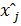 можем представить как значение, передаваемое СТС своим подсистемам.
можем представить как значение, передаваемое СТС своим подсистемам. 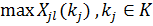
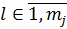
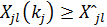
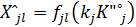
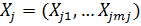
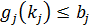 (11)
(11)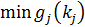
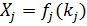
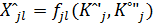 (12)
(12)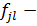 модель определяется параметром
модель определяется параметром 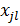 вектора
вектора 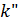 используется в качестве const при повторном уточнении решения задачи (10).
используется в качестве const при повторном уточнении решения задачи (10).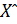 , затрат
, затрат 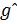 и показателей эфективности Wˆ.
и показателей эфективности Wˆ.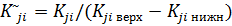 ,
, 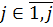 ,
, 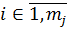
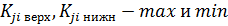 значения конструкторских параметров
значения конструкторских параметров 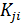 входящего в состав вектора
входящего в состав вектора 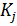
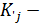 относятся те, для которых выполняется:
относятся те, для которых выполняется: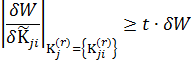
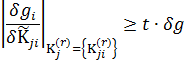
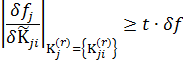
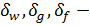 задаваемые значения чувствительности показателя эффективности затрат и ТТХ подсистем и применения конструктивных параметров.
задаваемые значения чувствительности показателя эффективности затрат и ТТХ подсистем и применения конструктивных параметров.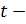 координирующий коэффициент.
координирующий коэффициент.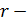 номер итерации.
номер итерации.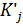 при фиксированных значениях параметров вектора вторичных параметров.
при фиксированных значениях параметров вектора вторичных параметров. 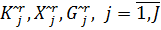 .
.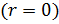 значения вектора
значения вектора 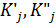 снова на основании (13)
снова на основании (13)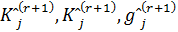 получены в ходе решения задания (11) и (12).
получены в ходе решения задания (11) и (12).
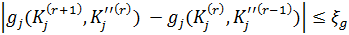
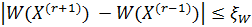
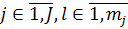 (14)
(14)