
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм классификации объектов. Метод шаров. В основе этого метода лежит геометрическая интерпретация близости объектов, оцениваемая функцией расстояния. В этом методе с геометрической интерпретацией последовательность оценок в
При этом любой объект изображается в виде точки в Евклидовом пространства, размерностью которого равно Для пояснения сути метода приведем геометрическую интерпретацию простейшего случая
Предположим, что известен некоторый радиус
Рис. 1. Геометрическая интерпретация метода шаров. На рис. 1. Показано расположение пяти точек объекта. После вычеркивания кругов и подсчета числа точек в каждом круге можно убедится, что при выбранном  Лучший объект для любого выделенного класса определяется в результате минимизации расстояния до идеального центра. В качестве идеального центра предлагается рассматривать точки в пространстве критериев Опишем теперь общий порядок действий, относящейся к пространству произвольной размерности. Дано множество: Для любой точки Эти точки образуют подмножество
Шар, который имеет максимальное число точек образует свое первое подмножество Разновидностью этого метода является метод тяжелого шара. Он состоит в следующем: В начале цент гипер-сферы помещают в произвольные точки пространства. Определяются объекты, которые оказались внутри этой гипер-сферы. Для этого вычисляется расстояние Для них вычисляются центр точек, и центр сферы перемещается в этот центр точек. Процедура смещения центра гипер-сферы радиуса Найденнаягипер-сфера образует подмножество Описанная процедура повторяется до тех пор, пока все исходное множество не будет разделено между классами. Радиус
Для многих объектов классификации характерно приблизительно небольшое изменение признаков от объекта к объекту. При этом совокупности объектов обычно образуют в гиперпространстве цепочки точек, в которые плохо укладываются в гипер-сферу. Удобной формной отображения закономерностей структура подобных множеств объектов могут служить цепь кратчайших незамкнутых путей.
Граф кратчайших незамкнутых путей характеризуется тем, что он соединяет все точки и при этом сумма длин всех его звеньев минимальна. Представления совокупности объектов в виде такого графа исключительно удобно, для моделирования структуры исходного множества объектов и анализа ее закономерностей.
Обобщённый образ группы Обобщённый образ – типовой объект, который характеризуется средними значениями признаков. Он может совпадать с одним из объектов данного класса, но может и не совпадать ни с одним из них и характеризоваться некоторыми средними значениями признаков. С группами, которые имеют большое количество объектов поступают так: Формулируется граф, любое звено которого представляет собой расстояние от исходных точек
Рассчитывается расстояние
Процедура
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 413. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
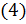 можно трактовать, как совокупность компонент вектора
можно трактовать, как совокупность компонент вектора 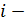 го объекта.
го объекта.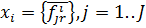
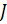 .
.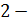 мерного пространства. В таком пространстве объекты исследуемого множества характеризуются только
мерного пространства. В таком пространстве объекты исследуемого множества характеризуются только 
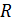 , соизмеримый со средним расстоянием между точками
, соизмеримый со средним расстоянием между точками 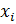 . Тогда из любой точки, как из центра можно построить круг, радиусом
. Тогда из любой точки, как из центра можно построить круг, радиусом 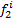
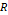

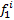
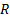


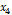

 лучший из этих трех ибо он ближе к центру (началу координат).
лучший из этих трех ибо он ближе к центру (началу координат).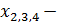 образ 1 класса,
образ 1 класса,  при этом оказывается самостоятельными классами.
при этом оказывается самостоятельными классами.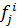 , координаты которого наибольше значению критерия заданной совокупности объекта данного класса.
, координаты которого наибольше значению критерия заданной совокупности объекта данного класса.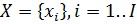
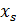 находящихся внутри любого шара.
находящихся внутри любого шара.
 подмножество, содержащие
подмножество, содержащие 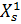 . В случае существования нескольких подмножеств с одинаковым номером точек, как и в прошлой задаче, выбирают подмножество близкое расположенное к началу системы координат. Далее выявляют другое подмножество, при этом из анализа исключаются объекты первого подмножества
. В случае существования нескольких подмножеств с одинаковым номером точек, как и в прошлой задаче, выбирают подмножество близкое расположенное к началу системы координат. Далее выявляют другое подмножество, при этом из анализа исключаются объекты первого подмножества  . Описанная процедура продолжается до момента полного исчерпания множество
. Описанная процедура продолжается до момента полного исчерпания множество 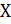 .
.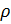 от центра гиперсферы до всех
от центра гиперсферы до всех 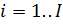 объектов. Те из них, для которых расстояние
объектов. Те из них, для которых расстояние 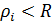 , считаются внутренними.
, считаются внутренними.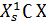 . Для определения, следующего подмножество точки класса
. Для определения, следующего подмножество точки класса 
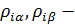 расстояния до точек
расстояния до точек 

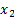
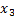
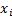
 до точек
до точек  .
.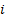
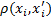

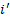
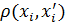 от исходного объекта
от исходного объекта 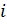 до остальных объектов данного класса и определяется сумма всех расстояний.
до остальных объектов данного класса и определяется сумма всех расстояний.
 число объектов в рассматриваемом классе.
число объектов в рассматриваемом классе.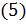 проводится для всех точек
проводится для всех точек 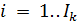 при этом, очевидно, что для одной из точек сумма расстояний
при этом, очевидно, что для одной из точек сумма расстояний 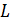 будет нашим оптимумом.
будет нашим оптимумом.  т.е.
т.е. 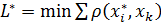 следующая точка
следующая точка 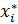 и будет искомой.
и будет искомой.