
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
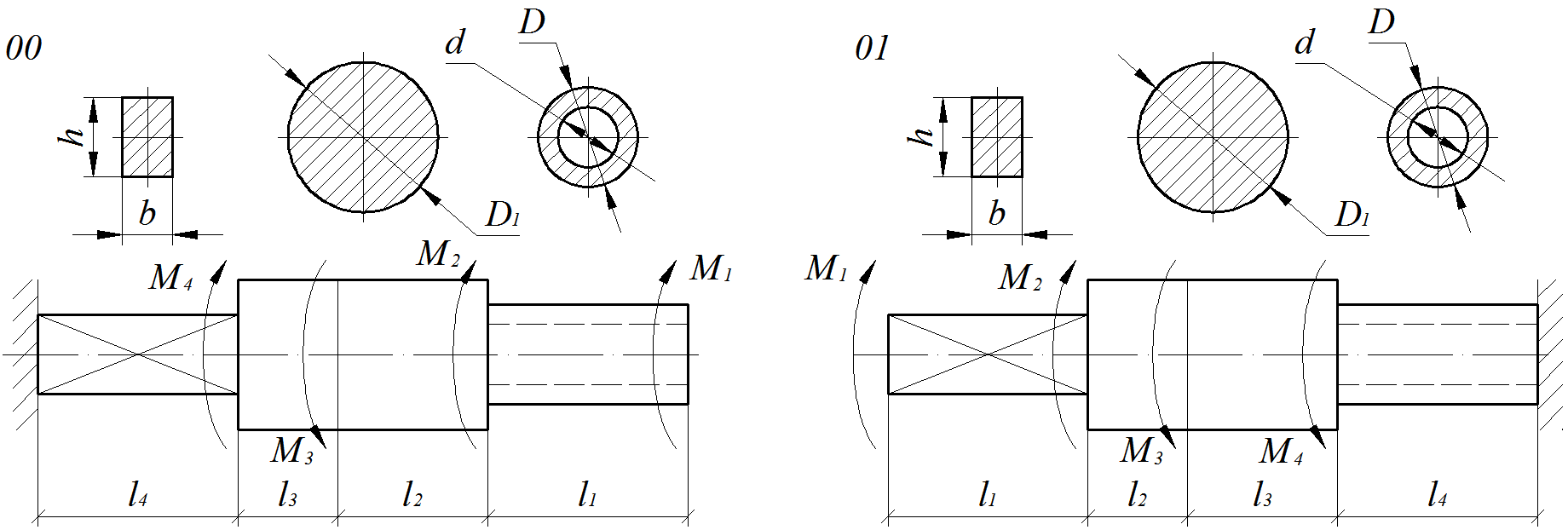
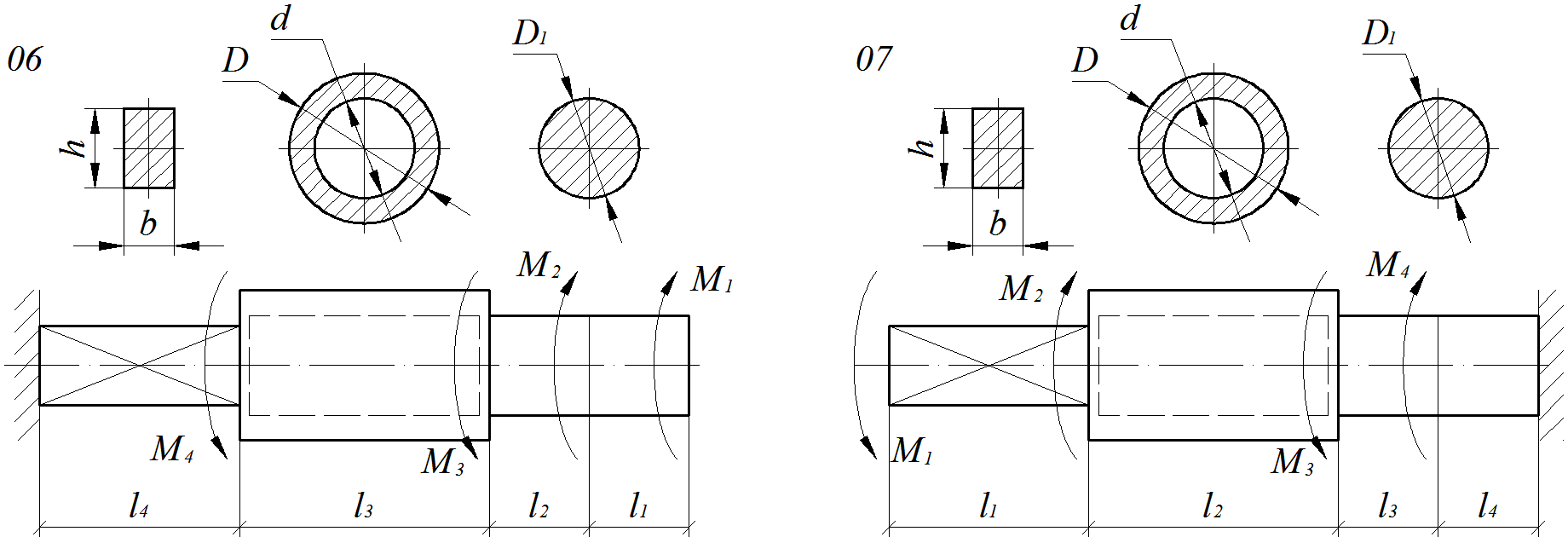
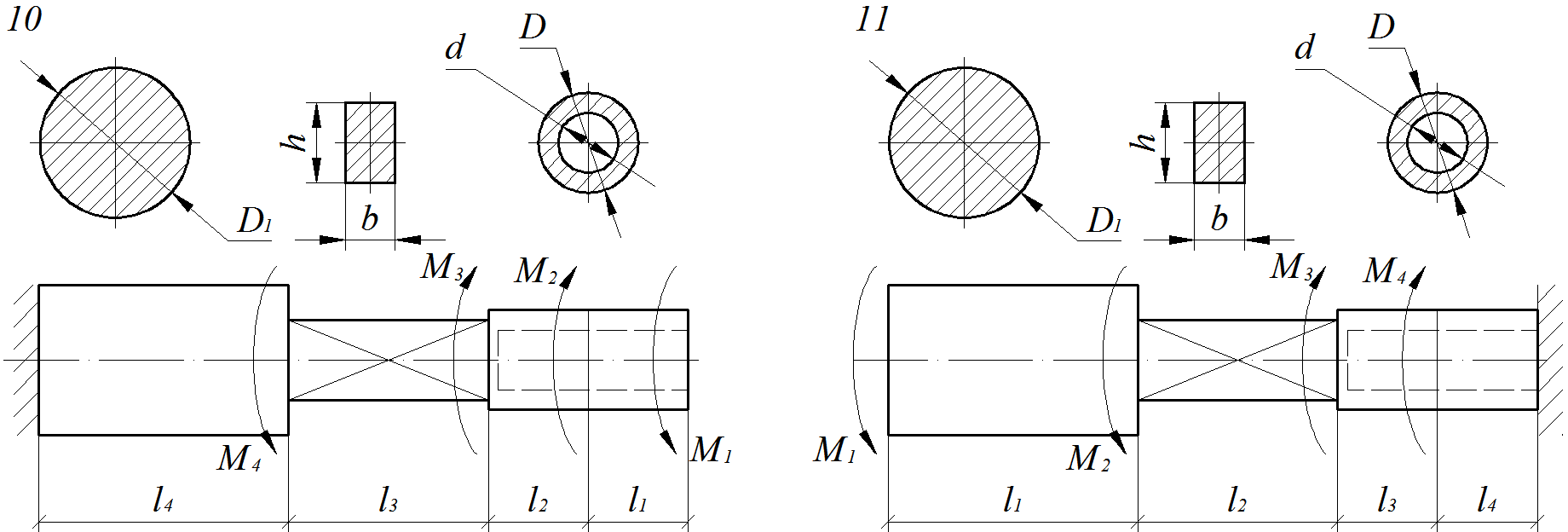
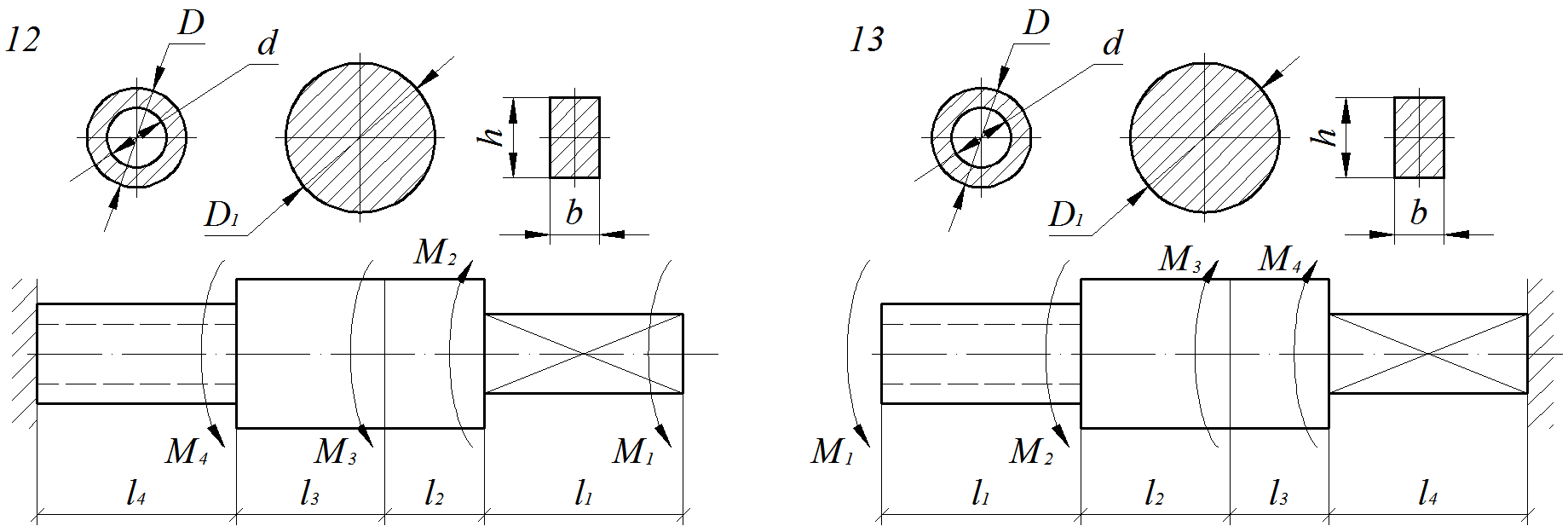
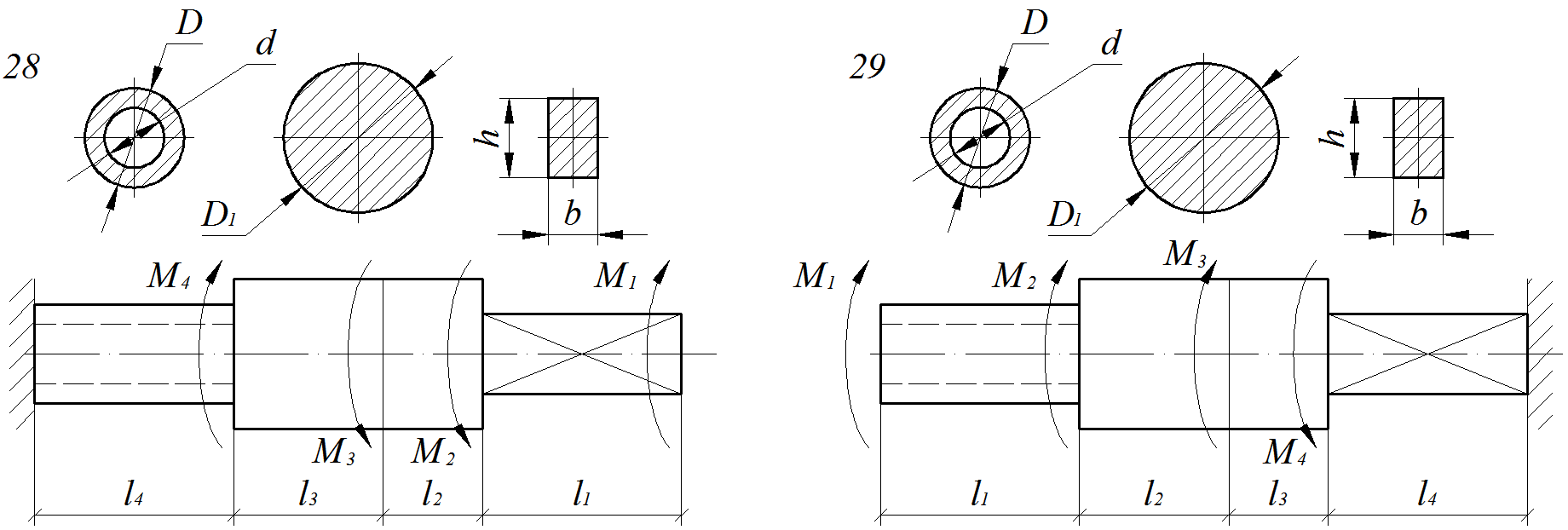
Расчет ступенчатого вала на прочность и жесткость при крученииМеталлический ступенчатый вал находится под действием сосредоточенных скручивающих моментов. Величины нагрузок, продольные размеры вала и соотношения размеров поперечных сечений приведены в табл. 4.1. Физико-механические характеристики материалов приведены в приложении А Для заданной схемы вала (рис. 4.1 – 4.4) требуется: 1) Составить аналитические выражения и построить эпюру крутящего момента; 2) Из расчета на прочность определить безопасные размеры поперечных сечений и округлить до размеров, кратных 5 мм; 3) В масштабе изобразить поперечные сечения вала на каждом силовом участке и построить эпюры распределения касательных напряжений; 4) Построить эпюру абсолютных углов закручивания по длине вала. Обязательно требуется соблюдать пропорции продольных размеров вала, размеров сечений при построении эпюр напряжений, а также, величин на эпюрах.При определении коэффициентов Эпюры, не подчиняющиеся правилам контроля эпюр при кручении[4, 5],преподавателем не рассматриваются. Таблица 4.1 Числовые данные для валов

Рис. 4.1
Рис. 4.2
Рис. 4.3
Рис. 4.4 Геометрические характеристики плоских сечений Используя данные табл. 5.1 для заданной схемы поперечного сечения (рис. 5.1 – 5.2), требуется: 1) Определить положение центра тяжести; 2) Вычислить центральные осевые моменты инерции; 3) Определить положение главных центральных осей инерции; 4) Вычислить величины главных центральных осевых моментов инерции и радиусов инерции; 5) Вычислить величины осевых моментов сопротивления. Расстояния до наиболее удаленных от главных осей точек определить построением; 6) Изобразить сечение в масштабе, показать на нем все используемые в расчетах размеры, оси положения центров тяжести и построить эллипс инерции. Таблица 5.1 Исходные данные для поперечных сечений
Рис. 5.1
Рис. 5.1
Плоское напряженное состояние в точке твердого тела Внутри тела, находящегося под действием внешних нагрузок, выделен бесконечно малый элемент объема в форме параллелепипеда с ребрами, параллельными координатным осям. На гранях параллелепипеда действуют известные напряжения
Рис. 6.1 Требуется: 1) Изобразить элемент объема, указав на нем истинные направления напряжений и учитывая, что 2) Определить аналитически и графически (с помощью круга Мора) главные напряжения 3) Определить аналитически и графически направление главных площадок; 4) Показать на рисунке положение элемента, ограниченного главными площадками, относительно координатных осей и направления главных напряжений; 5) Определить величины главных деформаций, относительное изменение объема тела, удельную потенциальную энергию в окрестности данной точки тела; 6) Проверить прочность в точке тела по I, II, III и IV теориям прочности. Числовые данные к задаче взять из табл. 6.1.
Таблица 6.1 Числовые данные к задаче |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 902. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
,  для прямоугольного сечения следует использовать линейную интерполяцию.Для стали принять во всех вариантах
для прямоугольного сечения следует использовать линейную интерполяцию.Для стали принять во всех вариантах  .
.


















 , мм
, мм






 ,
,  ,
,  ,
, 
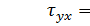 ;
; ,
,