Эквивалентность гравитационных сил

  и сил инерции

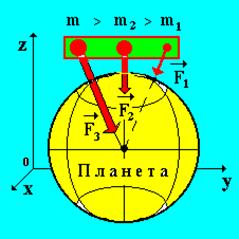
Принцип эквивалентности гравитационных сил и сил инерции установлен Эйнштейном.

Все физические явления в гравитационном поле происходят совершенно так же, как и в поле сил инерции, если напряженности обоих полей совпадают в соответствующих точках пространства, а начальные условия одинаковы для всех тел изолированной системы.

     Если тело свободно падает в гравитационном поле напряженности g, то это поле будет полностью компенсировано полем поступательных сил инерции.

Однако принцип эквивалентности гравитационных сил и сил инерции не утверждает, что всякое гравитационное поле может быть заменено полем сил инерции, а гравитационные силы – силами инерции.

Это связано с тем, что силы тяготения направлены к центру тяготеющей массы, например, Земли, т. е. являются центральными (рис. 31).

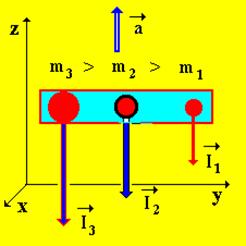
Ни какими ускоренными движениями системы отсчета нельзя этого получить.

Так как силы инерции будут всегда направлены параллельно друг другу (рис. 32).

Из принципа эквивалентности следует, что свойства пространства и времени в полях тяготения должны быть такими же, как и в неинерциональных системах отсчета.

Следовательно, в гравитационных полях, как и в неинерциальных системах отсчета, время неоднородно, а пространство является неевклидовым, неоднородным и неизотропным.

Тем самым подтверждено гениальное предвидение Н. И. Лобачевского, Римана и др., что геометрия реального мира может быть и неевклидовой.

По некоторым данным пространство не только искривлено, но и скручено.