
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Упругое столкновение в двух измерениях
При рассмотрении столкновений в двух измерениях необходимо учитывать векторный характер импульсов взаимодействующих частиц. Из всех случаев столкновений обычно рассматривают два: 1) одна частица (снаряд) сталкивается с другой частицей (мишенью), находящейся до взаимодействия в состоянии покоя; 2) импульсы частиц до столкновения направлены вдоль одной прямой. Если столкновение не лобовое, то в любом случае импульсы частиц после столкновения не совпадают с первоначальными их направлениями. В этом случае столкновение является двумерным, так как траектории взаимодействующих частиц лежат в плоскости, образованной первоначальными и конечными направлениями векторов импульсов частиц.
Рассмотрим столкновение частицы массой m1, движущейся вдоль оси Х со скоростью Например, для ядерных или электрически заряженных частиц процесс отклонения начинается до столкновения из-за существования ядерной или кулоновской силы, действующей между частицами. Расстояние r0 на рис. 19 называют прицельным параметром, который является мерой отклонения от лобового столкновения. При r0 = 0 столкновение является лобовым. Согласно закону сохранения импульса для изолированной системы, имеем а) на ось Х: б) на ось У: Применяя закон сохранения энергии, находим  Из полученных трех уравнений следует, что можно найти только три неизвестные величины. Если провести измерение, например угла a1, то переменные Все скорости и углы измеряются значительно раньше или значительно позже столкновения, пока не действуют (или уже не действуют) силы взаимодействия между частицами.
Неупругое столкновение
В результате неупругого столкновения двух макроскопических тел, они могут слипаться, и в дальнейшем будут двигаться как единое целое (рис. 20), где Из-за необратимой деформации они не восстанавливают своей формы. Энергия деформации переходит в теплоту Q. Считая систему двух тел замкнутой, применяем закон сохранения импульса в векторном виде: где
В проекции на ось Х mv1x+ Mv2x= (m + M)vx
или mv1 + Mv2 = (m + M)v. (39)
Формула (3.51) позволяет определить скорость слипшихся тел после их столкновения: Применяя общий закон сохранения энергии для такой системы, имеем
где Q – количество теплоты, выделившееся в результате деформации тел. Сечение рассеяния
Взаимодействие молекул и атомов характеризуют эффективным сечением (сечение рассеяния), которое зависит от характера сил взаимодействия между ними. Особую роль в атомной, ядерной физике и физике элементарных частиц играют эксперименты по рассеянию потока частиц мишенью. Рассеянием называют процесс столкновения потока одинаковых частиц, характеризующихся параллельными импульсами, с мишенью. При этом каждая частица из всего потока взаимодействует только с одной из частиц мишени, являющихся рассеивающими центрами (рис. 21). Поток падающих частиц называют пучком. Если частицы в пучке имеют не только параллельные импульсы, но и равные энергии, то такой пучок называют моноэнергетическим. Все процессы столкновения частиц с мишенью характеризуют сечением рассеивания s. В классической физике такое сечение рассеяния называют эффективным диаметром, т. е. s = pd2, где d – диаметр молекул.
Единичный акт столкновения частицы-снаряда с рассеивающим центром мишени, в результате которого частица отклоняется в пределах телесного угла dW, характеризуется дифференциальным сечением рассеяния где ds – дифференциальное сечение рассеяния, имеет размерность площади; dN – число частиц, рассеиваемых в единицу времени в элементарный телесный угол dW; r – плотность потока частиц, т. е. число частиц в пучке, пересекающих в единицу времени единичную площадку, перпендикулярную к направлению движения частиц. Так как dN ~ dW, то
По определению отношение dN/dW равно числу частиц, рассеиваемых в единицу времени в единичный телесный угол в направлении, которое определяется некоторыми углами q и j (рис. 22, где R – единичный радиус; 0 £ q £ p, 0 £ j £ 2p). Телесный угол dW на рис. 22 показан заштрихованной площадкой на сфере единичного радиуса, причем dW = sinqdqdj. Отношение dN/dW описывает угловое распределение рассеянных частиц (распределение по углам q и j). Поэтому Кроме дифференциального сечения рассеяния ds существует понятие полного сечения рассеяния Для определения сечения рассеяния достаточно знать только импульсы частиц. Координаты знать не обязательно. Поэтому понятие классического сечения рассеяния используют и в квантовой механике для описания столкновения микрочастиц. В ядерной физике единицей измерения сечения рассеяния является барн (1 барн = 10-24 см2). Это связано с геометрическими размерами ядер.
Для детального описания процесса рассеяния в классической физике используют прицельный параметр r0 (рис. 23), который равен наикратчайшему расстоянию, на котором частица-снаряд прошла бы от центра рассеяния в том случае, если бы взаимодействие между частицами отсутствовало. Анализ формулы (45) показывает, что полное сечение рассеяния имеет смысл площади, затеняемой центром рассеяния в направлении падения пучка. Частицы-снаряды пучка, нацеленные на мишень, будут рассеяны центром.
Следовательно, дифференциальное сечение рассеяния – часть площади s. В случае сферически симметричного рассеивающего центра она имеет форму кольца (рис. 24, а, б). Частицы, нацеленные в кольцо рассеиваются в некотором интервале углов, соответствующем значениям прицельного параметра, между внутренним, и внешним радиусами кольца. В процессе упругого рассеяния микрочастиц изменяются их импульсы. Наряду с этими процессами могут изменяться также внутренние состояния частиц (квазиупругие процессы) или образуются другие микрочастицы (неупругие процессы). ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ |
||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

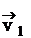 (импульсом
(импульсом  ), с покоящейся частицей массой m2 (рис. 19). После взаимодействия частицы разлетаются под углами a 1 и a2 относительно направления вектора импульса первой частицы, параллельного оси Х.
), с покоящейся частицей массой m2 (рис. 19). После взаимодействия частицы разлетаются под углами a 1 и a2 относительно направления вектора импульса первой частицы, параллельного оси Х. , где
, где  . Запишем закон сохранения импульса в проекциях:
. Запишем закон сохранения импульса в проекциях: ;
;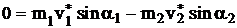 .
. .
. можно найти, используя полученные выше три уравнения.
можно найти, используя полученные выше три уравнения.
 .
. , (38)
, (38)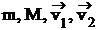 – массы и векторы скоростей тел до взаимодействия;
– массы и векторы скоростей тел до взаимодействия; – скорость слипшихся частиц после взаимодействия.
– скорость слипшихся частиц после взаимодействия.
 (40)
(40)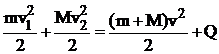 , (41)
, (41)
 (42)
(42)
 . (43)
. (43) . (44)
. (44) (45)
(45)
