
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Упругое взаимодействие двух частиц
Процесс упругого взаимодействия осуществляется в газах (столкновение молекул), ядерных реакциях (например, столкновение нейтрона с протоном). Упругим называют столкновение, в результате которого внутреннее состояние взаимодействующих частиц не меняется. Большинство упругих столкновений, за исключением ядерных реакций высоких энергий, относятся к медленным (нерелятивистским) процессам. Для расчета процесса упругого столкновения двух частиц применяют закон сохранения импульса и закон сохранения энергии. Для изолированной системы двух взаимодействующих частиц закон сохранения импульса запишем в виде где р1 = m1v1, p2 = m2v2 – импульсы частиц до взаимодействия (m1, m2 и v1, v2 – массы и скорости частиц до взаимодействия); Лабораторная система отсчета
Применяя закон сохранения центра масс (инерции) к системе двух частиц с учетом формул где Скорости частиц в ЛС можно выразить через скорость их центра инерции 
и векторы скорости частиц после взаимодействия Формулы (35) и (36) учитывают закон сохранения импульса для взаимодействующих частиц.
Система центра инерции В системе центра инерции (СЦИ) где - приведенная масса двух частиц. Подставив полученные значения импульсов в формулу (37), получим:
Из формулы (38) видно, что относительная скорость частиц до взаимодействия равна относительной скорости частиц после взаимодействия (v = v*), т.е. в результате столкновения частиц скорость относительного движения изменяет только свое направление, а по абсолютному значению остается неизменной (рис. 18). Угол q – называют углом рассеяния в СЦИ, и по величине он может быть любым. Если рассматриваемые частицы движутся навстречу друг другу с равными по величине, но противоположно направленными векторами импульсов Поэтому при упругом и лобовом столкновение двух частиц (бильярдные шары) они «отражаются» друг от друга и удаляются в противоположных направлениях с теми же по величине скоростями. Замечание: условие (39) выполняется и в случае неупругого столкновения частиц. Следовательно, как при упругих, так и неупругих столкновениях в СЦИ импульсы не зависят от угла. Если же столкновение не лобовое (рис. 18), то скорости частиц после взаимодействия остаются неизменными по величине, но направление векторов скоростей (импульсов) частиц после столкновения составляет некоторый угол Ðq с их первоначальным направлением (рис. 18). При упругом взаимодействии величины импульсов не изменяются, т. е. Таким образом, в СЦИ процесс взаимодействия характеризуется высокой степенью симметрии и поэтому анализ движения в ней осуществить проще, чем в любой другой системе отсчета (например, в экспериментах на накопительных кольцах частицы движутся навстречу друг другу с равными по величине, но противоположно направленными импульсами).
Если процесс столкновения частиц является упругим, центральным и происходит, например, вдоль оси Х (рис. 19), то для нахождения величин скоростей частиц после взаимодействия воспользуемся законом сохранения импульса в проекциях на ось Х и законом сохранения энергии в виде
так как Решая совместно выражения (33) и (34), имеем где Вывод: относительная скорость двух частиц до столкновения в точности равна их относительной скорости после столкновения. Такой вывод справедлив для любого лобового упругого удара независимо от того, какие массы имеют частицы. Выражая последовательно u2x и u1x из формулы (35) и подставив их значения в выражение (33), находим скорости частиц после взаимодействия: Рассмотрим некоторые частные случаи: 1. Если массы взаимодействующих частиц равны (m1 = m2), то u1x = v2x, u2x = v1x, т. е. частицы обмениваются скоростями. 2. Вторая частица до столкновения покоится (v2 = 0): а) если массы взаимодействующих частиц равны (m1 = m2), то u1x = 0 и u2x = v1x, т. е. первое тело останавливается после столкновения, а вторая частица начинает двига-ться со скоростью первой, какую она имела до столкновения; б) если m1 > m2, то первая частица продолжает двигаться в том же направлении, что и до удара, но с меньшей скоростью (u2 < v1), скорость второй частицы после удара увеличится, т. е. u2 > u1; в) если m1 < m2, то первая частица после столкновения изменит направление скорости (импульса) на противоположное, вторая частица начинает движение в том же направлении, в каком двигалась первая частица до столкновения; г) если m1 << m2 (случай упругого взаимодействия частицы с массивной неподвижной стенкой), то u1 = - v1, u2 = 0, т. е. направление скорости налетающей частицы после соударения со стенкой изменится на противоположное, а величина останется неизменной.
|
||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 628. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
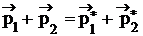 , (31)
, (31)  = m1u1,
= m1u1,  = m2u2 – импульсы этих же частиц после взаимодействия (u1, u2 – скорости частиц после взаимодействия). Закон сохранения энергии упругого столкновения двух частиц
= m2u2 – импульсы этих же частиц после взаимодействия (u1, u2 – скорости частиц после взаимодействия). Закон сохранения энергии упругого столкновения двух частиц  (32)
(32)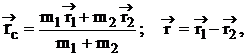 (33)
(33) – радиус-вектор центра масс;
– радиус-вектор центра масс;  ,
,  – радиус-векторы частиц в выбранной системе отсчета, имеем
– радиус-векторы частиц в выбранной системе отсчета, имеем (34)
(34)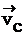 и скорости их относительного движения
и скорости их относительного движения  и
и  соответственно, до и после столкновения. Дифференцируя выражение (34) по времени и учитывая закон сохранения центра инерции (масс)
соответственно, до и после столкновения. Дифференцируя выражение (34) по времени и учитывая закон сохранения центра инерции (масс)  , находим векторы скорости частиц до взаимодействия
, находим векторы скорости частиц до взаимодействия (35)
(35) (36)
(36) = 0. Векторы импульсов взаимодействующих частиц в этой системе можно записать в виде
= 0. Векторы импульсов взаимодействующих частиц в этой системе можно записать в виде



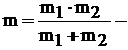 (37)
(37)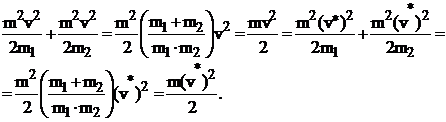 (38)
(38)
 , то суммарный импульс системы из двух частиц равен нулю, т. е.
, то суммарный импульс системы из двух частиц равен нулю, т. е.  (39)
(39) .
.
 (30) или
(30) или (31)
(31) , (32)
, (32) , векторы скорости всех частиц параллельны оси Х, то vy = 0, vz= 0 (
, векторы скорости всех частиц параллельны оси Х, то vy = 0, vz= 0 (  ) и, следовательно,
) и, следовательно,  . Формулы (31) и (32) преобразуем к виду
. Формулы (31) и (32) преобразуем к виду  (33)
(33) (34)
(34)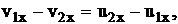 (35)
(35)  ,
,  – соответствующие проекции относительных скоростей на ось Х двух частиц до и после столкновения.
– соответствующие проекции относительных скоростей на ось Х двух частиц до и после столкновения. , (36)
, (36) . (37)
. (37)