Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сложное движение неинерциальной системы отсчета
Под сложным движением неинерциальной системы отсчета подразумевается ее одновременное поступательное и вращательное движение вокруг полюса (точки) с постоянной угловой скоростью. Согласно теореме Кориолиса: Вектор полного ускорения равен геометрической сумме векторов относительного, переносного и кориолисова ускорений. где вектор кориолисова ускорения
Вектор кориолисова ускорения равен удвоенному векторному произведению вектора угловой скорости и вектора относительной скорости. Ускорение Кориолиса возникает из-за изменения относительной скорости м. т. при переносном движении и переносной скорости при относительном движении. Абсолютная величина ускорения Кориолиса где w – угловая скорость вращения подвижной системы отсчета относительно неподвижной. Направление вектора ускорения Кориолиса можно получить, спроектировав вектор относительной скорости на плоскость, перпендикулярную к вектору угловой скорости, и повернув эту проекцию на угол 90О в направлении вращения. Вектор переносного ускорения Первое слагаемое мы рассмотрели выше. Второе слагаемое после взятия двойного векторного произведения получило название центростремительного ускорения, направленного по радиусу к оси вращения 
Центробежная сила инерции и сила Кориолиса
Найдем уравнение сложного движения. Умножим правую и левую части равенства (56) на массу м. т. (тела) m:
или где
– сила, возникающая в результате взаимодействия тел. – cила Кориолиса, перпендикулярна вектору угловой и вектору относительной скоростей; направлена противоположна вектору ускорения Кориолиса; определяется правилом правого винта; относится к гироскопическим силам и работы не совершает; возникает при вращении подвижной системы отсчета.
– центробежная сила инерции, возникающая при вращении подвижной системы отсчета. Свойства сил инерции
1. Силы инерции действуют только в неинерциальных системах отсчета. 2. Силы инерции вызваны не взаимодействием тел, а ускоренным движением системы отсчета. 3. К силам инерции не применим третий закон Ньютона, так как нет взаимодействующих тел. 4. Если некоторая система тел (м. т.) находится в неинерциальной системе отсчета, то силы инерции являются внешними силами, следовательно, системы не являются замкнутыми и поэтому не выполняются законы сохранения. 5. В неинерциальных системах отсчета силы инерции действуют точно также, как и силы взаимодействия тел, например, космонавт, весьма реально ощущает силу инерции, прижимающую его к креслу корабля, после старта ракеты на активном участке полета. 6. Силы инерции прямо пропорциональны массе тел. Поэтому в поле сил инерции все тела движутся с одинаковыми ускорениями (как и в поле сил тяготения).
Проявление сил инерции
Если пассажир находится в автомобиле или другом подобном транспорте, который начинает движение, быстро ускоряясь, то его прижимает к спинке сидения (пассажир сидит лицом в направлении движения) поступательная сила инерции, наоборот, если автомобиль резко тормозит, то пассажир наклоняется вперед. Когда автомобиль осуществляет поворот, то возникает центробежная сила инерции. Проявление центробежной силы инерции можно наблюдать на ряде опытов. Один из них приведен на рис. 27.
Как видно, чем дальше на нити груз находится от оси вращения, тем больше центробежная сила инерции и тем больше угол отклонения нити от вертикали. Проявление сил Кориолиса можно обнаружить на следующем примере. Если пассажир перемещается по салону автобуса, который производит поворот, то на него, кроме центробежной силы инерции, будет действовать и сила Кориолиса. В связи с этим легче удержаться, находясь в неподвижном состоянии. Чтобы найти траекторию движения тел под действием сил Кориолиса, проделаем такой опыт.
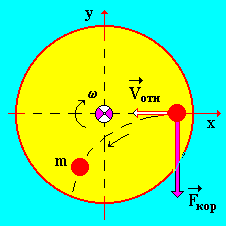
По полированной поверхности вращающегося диска, с постоянной угловой скоростью (гончарный круг, круг для полировки и огранке кристаллов и т. д.), катится в направлении к оси вращения с относительной скоростью шар массой m (рис. 28, вид сверху). В этом случае на него действует сила Кориолиса в направлении, указанном на рис. 28, по правилу правого винта. Вектор угловой скорости направлен от нас (на рис. 28 – обозначен крестиком). Если же шар будет катиться с относительной скоростью в направлении от оси вращения, то изменится и направление действия силы Кориолиса (рис. 29). На рис. 28 и рис. 29 траектория движения шара – пунктирная линия. Действие силы инерции испытывают летчики (перегрузки), выполняя фигуры высшего пилотажа. Силы инерции используют в центробежных машинах, насосах, сепараторах и т. д. Из-за вращения Земли вокруг своей оси любое свободно падающее тело в северном полушарии отклоняется к востоку и экватору. Реки, текущие с севера на юг в северном полушарии, подмывают западный берег, а в южном – восточный.
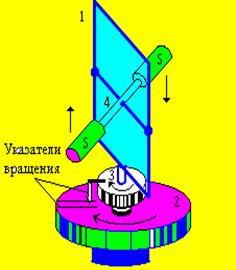
При движении поезда с юга на север больше изнашиваются правые рельсы. Неинерциальность систем отсчета можно проверить, используя маятники Фуко или Пошехонова. Действие маятника Фуко довольно подробно описано во многих учебниках и пособиях по физике. Поэтому рассмотрим принцип работы маятника Пошехонова. Он состоит из прямоугольной вертикальной рамки 1, установленной на вращающей подставке 2 (ось рамки закреплена в подшипнике 3). В центре рамки на горизонтальной оси закреплен в подшипниках стержень 4 с массивными грузами 5 на его концах равной массы, способный совершать колебательные движения. Сама подставка может быть приведена во вращение с помощью электромотора (рис. 30). Принцип действия маятника основан на законе сохранения момента импульса I1 w1 = I2 w2 = сonst. Приведем стержень с грузами 5 в колебательное движение. Одновременно включим электродвигатель (на рис. 30 не показан) и платформа 2 начнет вращаться с постоянной угловой скоростью.
Когда стержень занимает горизонтальное положение, а грузы максимально удалены от вертикальной оси, маятник поворачивается вместе с платформой с w1 (момент инерции I1 - максимален). В следующий момент времени стержень занимает вертикальное положение (момент инерции I2 минимален). Согласно закону сохранения импульса происходит возрастание угловой скорости w2, так как I2 < I1. Поэтому рамка при вращении обгонит платформу. Следовательно, будет наблюдаться поворот плоскости колебаний стержня-маятника. Этот прибор можно использовать для обнаружения проявления сил инерции, в том числе и при вращении Земли. В отличие от маятника Фуко эффект поворота плоскости колебаний стержня – маятника с помощью маятника Пошехонова достигается значительно быстрее.
|
||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 326. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (53)
, (53) . (54)
. (54) , (55)
, (55) . (56)
. (56)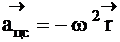 . (57)
. (57)


 (58)
(58)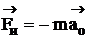 – поступательная сила инерции;
– поступательная сила инерции; (59)
(59)