Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Закон сохранения механической энергиии однородность времени Из свойства симметрии однородности времени следует, что законы движения замкнутой системы не зависят от выбора начала системы отсчета. Если в два произвольных момента времени все тела замкнутой системы поставлены в одинаковые условия, то, начиная с этих моментов времени, все явления в системе протекают одинаково. На основании классической механики Ньютона имеем А = Wk2 - Wk1. Силы, действующие на м. т., связаны с потенциальной энергией выражением где потенциальная энергия задана в виде функции состояния, т. е. Wp = Wp(x, y, z, t). Например, поле, где находится м. т., изменяется со временем (пульсирует). Тогда работа всех сил где Следовательно, или C другой стороны, полная работа A = DWk = Wk2 - Wk1. Cледовательно, (Wp2 + Wk2)-(Wp1 +Wk2) = В случае замкнутой системы, в силу однородности времени, производная потенциальной энергии по времени равна нулю, т. е. Таким образом, получаем закон сохранения механической энергии W = Wk + Wp = const. Замечание: В классической физике взаимосвязь кинетической энергии, импульса и массы описывается формулой Wk = p2 / (2m). В релятивистской физике согласно специальной теории относительности полная энергия частицы W = qmc2, р = qmv – импульс частицы, где  т. е. После преобразований получим формулу W2 = p2c2 + m2c4, которая выражает взаимосвязь массы, импульса и энергии, т. е. закон сохранения массы, импульса и энергии. Так как для частиц изолированной системы р = const (закон сохранения импульса) и W = const (закон сохранения механической энергии), то из последней формулы следует, что m = const и c = const. |
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 356. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
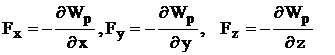 ,
,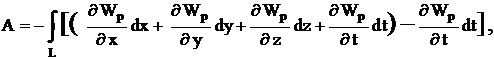
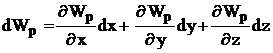 .
.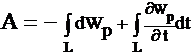
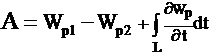 .
.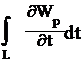 .
.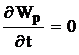 .
.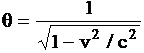 ,
,