Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Динамические свойства систем управления.Динамическая характеристика — это реакция системы на возмущение (зависимость изменения выходных переменных входных и от времени). Динамические характеристики определяют динамику системы, т.е. ее поведение в неустановившемся (переходном) режиме. При этом используют следующие основные динамические характеристики: 1. Передаточная функция системыW(p) есть отношение изображения выходной величины Y(p) к изображению входной величины X(t) при нулевых начальных условия: W(p)=Y/X. Основные свойства передаточной функции: 2. Временной характеристикой системыназывается закон изменения выходной величины в функции времени при изменении входного воздействия по определенному закону и при условии, что до приложения воздействия система находилась в покое. Временные характеристики определяются как реакция системы на типовые воздействия при нулевых начальных условиях.  Ступенчатое воздействие: Единичный импульс. Единичный импульс(d – функция) – это идеализированный сигнал, который характеризуется бесконечно малой длительностью, бесконечно большим уровнем (амплитудой) и площадью равной единице. Линейно-растущее воздействие – это воздействие с постоянной скоростью изменения сигнала. Такое воздействие чаще всего используется для определения точности систем и описывается соотношением: Квадратичное воздействие – это воздействие с постоянным ускорением изменения сигнала. Такое воздействие чаще всего используется для определения точности систем и описывается соотношением: 3. Частотные характеристики определяются, как реакция системы на гармоническое типовое воздействие при нулевых начальных условиях.
При подаче на вход системы гармонического воздействия
При изменении частоты получим следующие частотные характеристики:
Второй метод Ляпунова. ИЗ ИНЕТА При исследовании устойчивости прямым методом Ляпунова, именуемым также второй методой Ляпунова, предполагается использование непрерывной скалярной функции переменных состояния V(x) совместно с уравнениями состояния где fi - нелинейные функции произвольного вида, удовлетворяющие условию f1 = f2 = ... = fn = 0 при x1 = x2 = ... = xn = 0, (10.2) так как в установившемся состоянии все отклонения и их производные равны нулю. Чтобы исследовать устойчивость по Ляпунову, необходимо подобрать некоторую знакоопределенную функцию V(x) и вычислить производную по времени от этой функции W(x).
ИЗ ЛЕКЦИЙ Маликова Система дифференциальных уравнений возмущенного движения
(f удовлетворяет условиям существования, единственности и нелокальной продолжимости решений, непрерывной зависимости от начальных данных (и времени t) Теорема 1.Для устойчивости (соответственно устойчивости, равномерной по t0 )невозмущенного движения x=0 системы (1,1) необходимо и достаточно, чтобы в некоторой области Г1 существовала непрерывно дифференцируемая определенно положительная (соответственно и допускающая бесконечно малый высший предел) функция v(t,x), производная которой в силу (1.1) постоянно отрицательна
Теорема 2.Для равномерной асимптотической устойчивости решения x=0 системы (1.1) необходимо и достаточно, чтобы в некоторой области Г1существовала непрерывно дифференцируемая положительно определенная функция v(t,x), допускающая бесконечно малый высший предел, производная которой в силу системы (1.1) определенно отрицательна. ИЗ КНИЖКИ 2-метод Ляпунова Второй (прямой) метод Ляпунова основывается на построение специальных функций Ляпунова, позволяющих получить достаточные условия устойчивости равновесия в большом. В его основе лежат две теоремы Ляпунова, приводимые без доказательства.
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. 
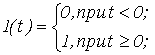

 . (7)
. (7) . (9)
. (9) Пусть задана система (рис. 7) с передаточной функцией K(p).
Пусть задана система (рис. 7) с передаточной функцией K(p). , (17) на выходе получим
, (17) на выходе получим  (18)
(18) 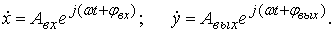 (19)
(19) 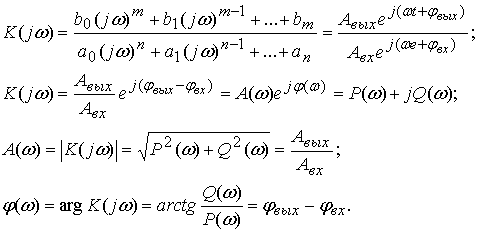 (20)
(20) АФХ – амплитудно-фазовая частотная характеристика;
АФХ – амплитудно-фазовая частотная характеристика;  ВЧХ – вещественная частотная характеристика;
ВЧХ – вещественная частотная характеристика; 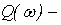 МЧХ – мнимая частотная характеристика;
МЧХ – мнимая частотная характеристика;  АЧХ – амплитудно-частотная характеристика;
АЧХ – амплитудно-частотная характеристика;  ФЧХ – фазовая частотная характеристика.
ФЧХ – фазовая частотная характеристика.  при i = 1, 2, ... , n, (10.1)
при i = 1, 2, ... , n, (10.1)