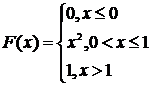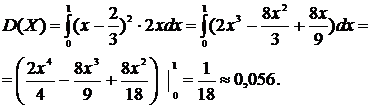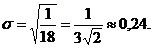Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
РАСПРЕДЕЛЕНИЕ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.
Для непрерывной случайной величины невозможно описать закон распределения с помощью таблицы, в которой были бы перечислены все возможные значения этой величины и их вероятности. Однако различные области возможных значений этой величины все же не являются одинакого вероятными. т.е. и для непрерывной случайной величины существует свое “распределение вероятностей”, хотя и не в том смысле, как для дискретной величины. 1. Функцией распределения непрерывной случайной величины Х называется функция F(x) равная вероятности того, что случайная величина приняла значение, меньшее х: F(x) = P(X< x) . Функцию F(x) называют еще интегральной функцией распределения.
Геометрически это равенство можно истолковать так: функция F(x) есть вероятность того, что случайная величина Х (случайная точка Х на оси Ох ) в результате опыта попадет левее точки х (рис. 3.). Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения. Причем она существует для всех случайных величин, как дискретных, так и непрерывных.
Рис. 3. Геометрический смысл функции распределения непрерывной случайной величины.
2. Основные свойства функции распределения:
1) Функция распределения принимает значения в интервале (0; 1): 0 ≤ F(х) ≤ 1. 2) F(x) - неубывающая функция, т.е. если х2 > х1 , то и F(х2 ) > F(х1). 3) Если все возможные значения непрерывной случайной величины X принадлежит интервалу (a; b), то: F(x) = 0 при x ≤ a; F(x) =1 при x ≥ b.
Следствие. Если возможные 
Это значит, что график функции распределения расположен в полосе, ограниченной прямыми y=0 и y=1.
3. Функцию f(x), равную производной ее интегральной функции распределения F(x) называемой плотностью распределения(или плотностью вероятности) непрерывной случайной велечины X: f(x)=F/(x). Поэтому функцию f(x) называют дифференциальной функцией распределения .
4. Кривая у=f(x), изображающая плотность распределения случайной величины называемой кривой распределения. 5. Основные свойства функции распределения:
1) Функция f(x) является неотрицательной: 2) Вероятность того, что непрерывная случайная величина в результате испытания примет какое-либо значение из интервала (а,в) равна определенному интегралу от плотности вероятности в пределах от а до в: то Т.о. вероятность того, что случайная величина примет значение, заключенное в интервал (а; в), равна приращению функции распределения на этом интервале F(в) - F(а).
Геометрически это выражение можно обосновать так (рис. 4.): вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а; в) численно равна площади криволинейной трапеции, ограниченной осью Ох, прямыми х=а, х=в и кривой f(x).
Следствие 1. Заменив пределы интегрирования а на Следствие 2. Несобственный интеграл от функции плотности распределения равен 1.
Это равенство называют условием нормировки плотности вероятности.
Рис. 4. Геометрический смысл функции плотности вероятности непрерывной случайной величины.
6. Числовые характеристики непрерывной случайной величины X с плотностью распределения f(x) определяющая аналогично числовым характеристикам дисперсных случайных величин (за исключением моды и медианы). · Математическим ожиданиемнепрерывной случайной величины X, возможные значения которой принадлежат отрезку (а;в) называют величину определенного интеграла: Название математического ожидания – центр распределения вероятностей случайной величины Х для непрерывных случайных величин даже более актуально, чем для дискретных.
· Дисперсией непрерывной случайной величины Х, возможные значения которой принадлежат отрезку (а; в), называют величину определенного интеграла: где
· Среднее квадратичное отклонение нерперывной случайной величины
Пример 15. Непрерывная случайная величина задана функцией распределения
Найти М(Х), D(X), σ.
Решение. 1) Найдем функцию плотности вероятности 2) 3) 4)
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 значения непрерывной случайной велечины расположены на всей числовой оси, то справедливы следующие предельные соотношения :
значения непрерывной случайной велечины расположены на всей числовой оси, то справедливы следующие предельные соотношения :
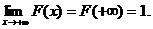
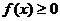
 ; так как f(x)=F/(x),
; так как f(x)=F/(x),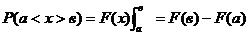
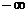 , в на х получим интеграл с переменным верхним пределом, который равен функции распределения этой случайной величины.
, в на х получим интеграл с переменным верхним пределом, который равен функции распределения этой случайной величины. 
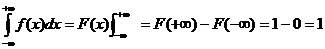 .
.
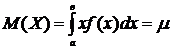 , где f(x) - плотность вероятности.
, где f(x) - плотность вероятности.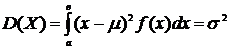 ,
, - математическое ожидание ; f(x) - плотность вероятности.
- математическое ожидание ; f(x) - плотность вероятности. .
.