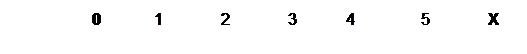Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН.
Закон распределения случайной величины не всегда бывает известен. В этом случае для описания случайной величины достаточно бывает указать её числовые характеристики, которые выражают наиболее существенные особенности распределения. К числовым характеристикам относятся: математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение.
1. Математическим ожиданием дискретной случайной величины X называют сумму произведений всех возможных значений случайной величины Х на вероятность этих значений:
Математическое ожидание - центр распределения и его можно рассматривать как "истинное'' значение случайной величины. При большом числе испытаний n среднее арифметическое значение случайной величины близко к ее математическому ожиданию. Пусть Х принимает значение x1 m1 раз, значение x1 - m1 раз, и т.д.; причем m1+m2+...mn= n, тогда:
При большом числе испытаний n их относительная частота
2. Основные свойства математического ожидания: 1) Математическое ожидание постоянной величины равно этой постоянной: M(C) = C. 2) Постоянный множитель можно выносить за знак математического ожидания: M(CX) = С*M(X), где с = const. 3) Mатематическое ожидание суммы случайных величин X и Y равно сумме их математических ожиданий:
4) Mатематическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M (X
3. Модой М0 дискретного распределения случайной величины называют такое значение случайной величины, которому соответствует наибольшая вероятность.  4. Медианой Ме дискретного распределения случайной величины называют серединное значение между наименьшим и наибольшим значениями случайной величины. Кроме математического ожидания мода и медиана являются характеристиками положения случайной величины. 5. Часто бывает необходимо знать степень рассеяния (разброса) случайной величины около математического ожидания. Для этого используют понятие дисперсии дискретной случайной величины. Дисперсия D(X) равна математическому ожиданию квадрата разности случайной величины и ее математического ожидания :
где Учитывая определение математического ожидания
Иначе дисперсияравна разности математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины:
Эти формулы можно применять для вычисления дисперсии равнозначно, т.к.
6. Свойства дисперсии случайной величины:
1) Дисперсия постоянной величины равна нулю, т.е. постоянная величина дисперсии не имеет: D(С) = 0. 2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(С*X) = 3) Дисперсия суммы или разности двух независимых случайных величин равна сумме дисперсий этих величин : D( 7. Дисперсия имеет размерность квадрата случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используют среднее квадратичное значение
1) М0 = 2, т.к. вероятность для этого значения случайной величины наибольшая (p2 = 0,4). 2) Ме = 3 – это середина отрезка (1; 5). 3) M(Х)= 4) 5) D(x)=M( 6)
Рис.2. Расположение числовых характеристик на числовой прямой. |
|||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 333. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

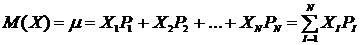 .
.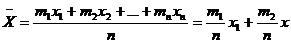
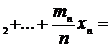
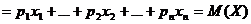 .
.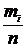 стремится к вероятности p1 (статистическое определение вероятности).
стремится к вероятности p1 (статистическое определение вероятности).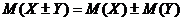 .
. Y) =M (X)
Y) =M (X) 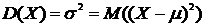 ,
,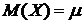 - математическое ожидание случайной величины, и величина
- математическое ожидание случайной величины, и величина 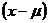 - это центрированная случайная величина или отклонение.
- это центрированная случайная величина или отклонение.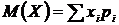 , можно записать для дисперсии:
, можно записать для дисперсии: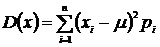 .
.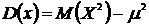 .
.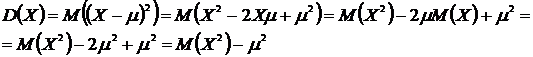
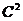 *D(X).
*D(X).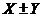 )=D(
)=D( 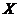 )
) 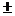 D(
D( 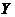 ).
).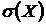 :
: 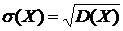 .
. Пример 14. Пусть закон распределения случайной величины задан следующей таблицей:
Пример 14. Пусть закон распределения случайной величины задан следующей таблицей: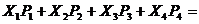
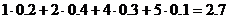 .
.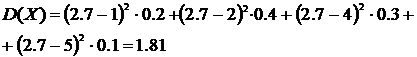 или
или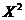 ) -
) - 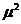 =
= 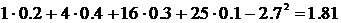
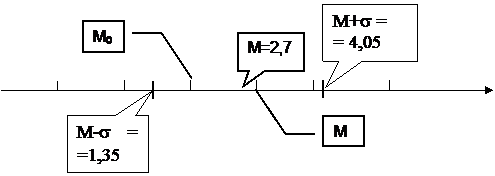
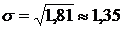 М ± s = 2,7 ± 1,35
М ± s = 2,7 ± 1,35