
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Т2.Вероятность произведения двух независимых событий A и B равна произведению вероятности этих событий.P(A * B) = P(A) * P(B).
Иначе: Вероятность произведения равна произведению вероятностей.
С.2.1.При независимых событиях А1, А2,,…, Аn вероятность их произведенияя равна произведению соответствующих вероятностей: P(A
Пример 6. Медицинская сестра обслуживает 4 палаты. Вероятность того, что в течение часа последует вызов сестры в первую палату P(1) = 0,2; во вторую палату P(2) = 0,3; в третью палату P(3) = 0,1; в четвертую палату P(4) = 0,25 . Какова вероятность того, что в течение часа последуют вызовы во все четыре палаты? P(1*2*3*4) = P(1) * P(2) * P(3) * P(4) = 0,2 * 0,3 * 0,1 * 0,25 = 0,0015
С.2.2.Вероятность осуществления хотя бы одного из событий A
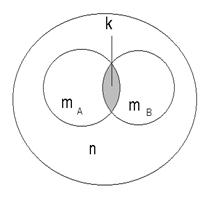
Т3 Вероятность наступления хотя бы одного из двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного наступления: Р(А+В)=Р(А)+Р(В)-Р(АВ) Р(А или В)=Р(А)+Р(В)-Р(АВ)
Доказательство этой теоремы можно проиллюстрировать исходя из геометрической интерпретации. На рисунке: · n-общее число всевозможных элементарных событий, · mА - число исходов, благоприятствующих появлению события А, · mB - число исходов, благоприятствующих появлению события В, · к – число исходов, благоприятствующих одновременному наступлению событий А и В, ·
тогда m=mА+mВ-к - число исходов, благоприятствующих появлению либо события А, либо cобытия В, т.к. область к в площади фигуры, получающейся пересечением должна учитываться только один раз.
Т4.Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, причем очередность появления этих событий не играет роли:  P(A * B) = P(A) * P(B/А) = Р(В)*Р(А/В).
С.4.1.В случае нескольких зависимых друг от друга событий вероятность их одновременного наступления будет равна произведению вероятности первого события на вероятность всех последующих событий, вычисленную при условии, что все предыдущие события произошли: Т5. Вероятность события А, которое может осуществиться лишь при условии осуществления хотя бы одного из несовместных событий
С.5.1.Условная вероятность события Вероятности, вычисляемые по формуле Бейеса часто называют вероятностями гипотез. Формула Бейеса позволяет переоценить вероятности гипотез, принятые до испытания, по результатам уже проведенного испытания. ФОРМУЛА БЕРНУЛЛИ
1. При практическом использовании теории вероятностей особое значение имеют события, связанные с независимыми повторными испытаниями, для которых выполняются условия:
Пример 7. 1. При подбрасывании монеты выпадение "орла" и "решки" удовлетворяют этим условиям. 2. Многолетние наблюдения показывают, что в течении дня соль приобретают 10% покупателей бакалейного отдела. Какова вероятность, что из 100 покупателей, приобретающих товар в бакалейном отделе равно 10 будут покупать соль?
То есть во многих задачах требуется найти не вероятность каждого отдельного события, а вероятность осуществления события А ровно m раз в данной серии из n испытаний. Для этого пользуются формулой Бернулли.
Здесь: р - вероятность появления события А в отдельном испытании; q - вероятность противоположного события q=1- p;
Пример 8. Вернемся к предыдущему примеру с покупателями соли. Вероятность покупки соли отдельным покупателем р=0,1, значит вероятность противоположного события, т.е. того, что соль не будет куплена q=1-p=1-0,1=0,9. Общее число покупателей n=100, число предполагаемых покупателей соли m=10, поэтому n-m=100-10=90. Подставляем данные в формулу Бернулли:
Вероятность того, что из данных 100 покупателей соль приобретут ровно 10 человек равна 13%, хотя по статистике только каждый 10-ый покупатель приобретает в этом отделе соль.
2. Частные случаи формулы Бернулли:
1. Вероятность осуществления события n раз в n испытаниях (m = n): 2. Вероятность осуществления события А ноль раз в n испытаниях (m = 0): 3. Вероятность осуществления события А не более m раз в n испытаниях: 4. Вероятность осуществления события А не менее m раз из n испытаний: Пример 9. Найти вероятность того, что в семье, имеющей пять детей, будет: 1) две девочки; 2) не менее двух девочек; 3) не более 4х девочек. Считать вероятность рождения мальчика pм= 0,4 и девочки pд= 0,6. Решение. Общее количество детей n=5, вероятность рождения девочки p=0,6, значит вероятность рождения мальчика, т.е. не девочки q=1-0,6=0,4;
1) m=2. 2) m³2.
3) m£4.
или, что тоже самое
3. При большом числе n повторных испытаний некоторого события А формулой Бернулли пользоваться сложно. В этом случае используют формулу Лапласа. Если вероятность осуществления события А в n испытаниях отличны от 0 и 1, то вероятность, что это событие осуществиться равно m раз равна значению функции:
где аргумент функции Пример 10. Вероятность заболевания туберкулезом легких в некоторой местности 0,003. Какова вероятность того, что при осмотре 1000 человек будет выявлено 3 больных?
m=3 p=0,003
4. Формула Лапласа непригодна при малых значениях вероятности события А в одиночных испытаниях , (т.е. при р где
Пример 11. Фармацевтический завод отправил на аптечный склад 10 000 ампул димедрола. Вероятность того, что в пути ампула будет повреждена 0.0002. Найти вероятность того, что на склад поступить 5 ампул поврежденных из этой серии.
6.Наивероятнейшим числом появления события называется такое число повторений события, вероятность которого наибольшая.
По определению наивероятнейшее число появлений события К0 должно удовлетворять двум неравенствам:
Рn(K0) Pn(K0)
Решая эти неравенства, получаем: K0 K0 или двойное нерaвенство: (np – q)
Равенство имеет место, если (np - q) – целое число; тогда в этом случае К0 имеет два значения: K0=(np - q) и K0= (np + p). Если же (np - q) – дробное число, то между числами (np - q) и (np + p) заключено единственное целое число К0. Если (np)- целое число, то К0=np.
Примеры 12. 1. Вероятность производства нестандартной детали р=0,022. Найти наивероятнейшее число нестандартных деталей в партии на 500 деталей.
N=500 n*p-q=500*0.022-0,978=11-0,978=10,022 P=0.022 n*p+p=500*0.022+0.022=11.022 Q=0.978 10.022
2. Вероятность попадания в цель при одном выстреле из орудия равна 0,2. Найти наивероятнейшее число попаданий в цель, если будет сделано 14 выстрелов.
N=14 n*p-q=14*0.2-0.8=2.8-0.8=2.0 P=0.2 n*p+p=14*0.2+0.2=2.8+0.2=3.0 Q=0.8 K0=2; K0=3
3. Найти наивероятнейшее число выпадения герба при 100 подбрасываниях монеты.
N=100 n*p=100*0.5=50 n*p-q=50-0.5=49.5 P=0.5 K0=50 n*p+q=50+0.5=50.5
K0=50
|
|||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 292. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
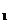 ×A
×A 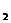 × …× A
× …× A 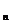 ) = P(A
) = P(A 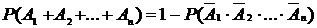
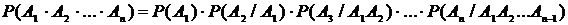
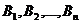 , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий 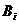 на соответствующую условную вероятность события А .
на соответствующую условную вероятность события А .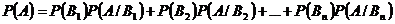
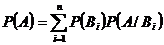 - эта формула называется формулой полной вероятности.
- эта формула называется формулой полной вероятности.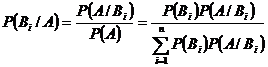
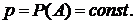
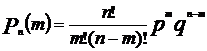
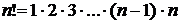 (читается «эн факториал» - произведение последовательных натуральных чисел от 1 до n, например 5!=1×2×3×4×5=120).
(читается «эн факториал» - произведение последовательных натуральных чисел от 1 до n, например 5!=1×2×3×4×5=120).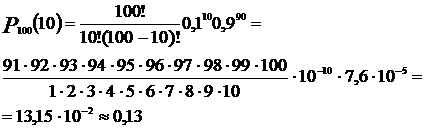
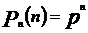 .
.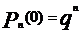 .
.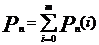 .
.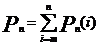 .
.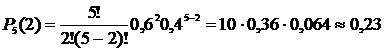
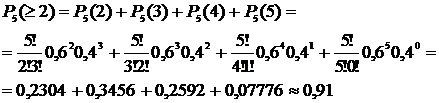
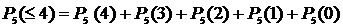
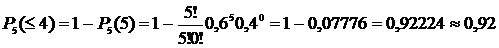

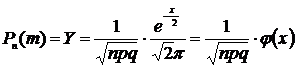 ,
,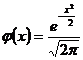 -функция Лапласа,причем
-функция Лапласа,причем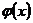 -функция четная и для определения ее значений есть таблица (табл. 1.);
-функция четная и для определения ее значений есть таблица (табл. 1.);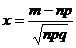 .
. n=1000 Р1000(3) =
n=1000 Р1000(3) = 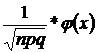 , где
, где 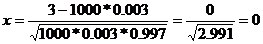 ,
, 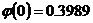
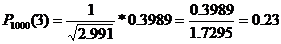 .
.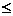 0.1). В этом случае пользуются законом редких событий (законом Пуассона):
0.1). В этом случае пользуются законом редких событий (законом Пуассона):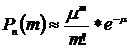 ,
,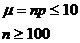

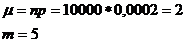
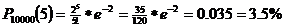
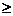 Pn(K0+1)
Pn(K0+1)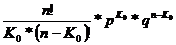
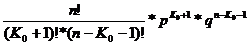

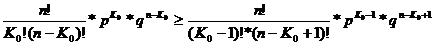



 Q=0.5 49.5
Q=0.5 49.5