
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометричне розв’язання задач нелінійного програмування. ⇐ ПредыдущаяСтр 9 из 9 Загальних методів розв’язання задач нелінійного програмування не існує, тому майже завжди такі задачі вимагають творчого підходу. Іноді геометричний метод дозволяє розв’язати і задачі нелінійного програмування. Деякі випадки такого типу розглянемо на прикладах. Приклад 6. Знайти найбільше значення функції
Знайдемо опорні прямі, які визначаються лінійною формою цільової функції. Для цього із сімейства паралельних прямих Пригадаємо, що дотична до кола в точці дотику перпендикулярна до радіуса. А це означає, що радіус Тепер координати точки
Остаточно одержуємо: Відповідь:,
Приклад 7. Знайти найбільше і найменше значення функції
Розв’язання. Спочатку визначимо графічно множину допустимих планів. Це буде множина точок у першому квадранті, задана трикутником
Тепер перетворимо цільову функцію до такого виду:  Отже маємо:
Оскільки ця похідна приймає тільки від’ємні значення, то це означає, що функція Точка Точка Відповідь:
Приклад 8. Знайти найбільше і найменше значення функції
Перетворимо тепер цільову функцію до такого виду:
Тобто, при Тепер легко бачити, що мінімальне значення цільова функція набуває в точці Відповідь: Приклад 9. Знайти найбільше і найменше значення функції
Побудуємо лінію рівня цільової функції. Ця лінія визначається рівнянням
Це буде коло з центром в точці Отже, Відповідь:
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 182. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 при обмеженнях:
при обмеженнях:
 Розв’язання. Спочатку побудуємо графічно множину допустимих планів. Це буде множина точок чверті кола радіуса 6 з центром в початку координат, яка лежить у першому квадранті:
Розв’язання. Спочатку побудуємо графічно множину допустимих планів. Це буде множина точок чверті кола радіуса 6 з центром в початку координат, яка лежить у першому квадранті: . Тепер легко бачити, що мінімальне значення цільова функція набуває при
. Тепер легко бачити, що мінімальне значення цільова функція набуває при  , а для визначення точки максимуму треба визначити координати точки
, а для визначення точки максимуму треба визначити координати точки  , тобто координати точки дотику до кола прямої, яка паралельна прямій рівня
, тобто координати точки дотику до кола прямої, яка паралельна прямій рівня  .
. буде перпендикулярним і до прямої
буде перпендикулярним і до прямої  . Відомо, що кутові коефіцієнти двох взаємно перпендикулярних прямих задовольняють умові:
. Відомо, що кутові коефіцієнти двох взаємно перпендикулярних прямих задовольняють умові:  , звідки
, звідки  , а рівняння прямої
, а рівняння прямої  .
. Þ
Þ 
 .
.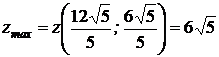 .
.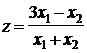 при обмеженнях:
при обмеженнях:
 :
:
 .
. . Тобто,
. Тобто,  лінійно залежить від
лінійно залежить від  . При цьому відповідна пряма проходить через початок координат, а її кутовий коефіцієнт залежить від
. При цьому відповідна пряма проходить через початок координат, а її кутовий коефіцієнт залежить від  :
:  . Проаналізуємо тепер, як саме
. Проаналізуємо тепер, як саме  залежить від
залежить від  :
: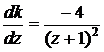 .
. спадна. Тобто, при зростанні
спадна. Тобто, при зростанні  зменшується. Отже, цільова функція
зменшується. Отже, цільова функція  і досягає максимуму в точці
і досягає максимуму в точці  . Знайдемо координати цих точок і відповідні значення цільової функції.
. Знайдемо координати цих точок і відповідні значення цільової функції. .
. .
.  ,
, 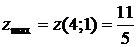 .
.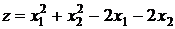 при обмеженнях:
при обмеженнях:
 Розв’язання. Визначаємо графічно множину допустимих планів. Це буде множина точок у першому квадранті, яка задана трикутником
Розв’язання. Визначаємо графічно множину допустимих планів. Це буде множина точок у першому квадранті, яка задана трикутником  :
: .
. відповідна лінія рівня є коло. Рівняння цього кола має такий вид:
відповідна лінія рівня є коло. Рівняння цього кола має такий вид:  . Центр цього кола знаходиться в точці
. Центр цього кола знаходиться в точці  , а радіус
, а радіус  залежить від
залежить від  .
. :
:  ,
,  . В точці
. В точці  :
:  ,
,  . В точці
. В точці  ,
,  . І нарешті в точці
. І нарешті в точці  ,
, 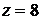 .
. ,
, 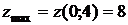 .
. при обмеженнях:
при обмеженнях:
 Розв’язання. Побудуємо спочатку множину допустимих планів задачі. Це буде перетин півплощин, яки визначаються нерівностями системи обмежень задачі. Це буде многокутник
Розв’язання. Побудуємо спочатку множину допустимих планів задачі. Це буде перетин півплощин, яки визначаються нерівностями системи обмежень задачі. Це буде многокутник  .
. .
. радіуса
радіуса 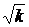 . На цьому колі значення функції сталі і дорівнюють
. На цьому колі значення функції сталі і дорівнюють  , коли радіус дорівнює нулю. Найбільше значення функція приймає в точці многокутника
, коли радіус дорівнює нулю. Найбільше значення функція приймає в точці многокутника  .
. ,
,  ,
,  ,
,  .
. .
.