
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постановка основної задачі лінійного програмування (ЗЛП).Задачі лінійного програмування є окремим випадком задачі математичного програмування. Вони отримали найбільше практичне застосування, їх розв’язання найповніше математично розроблено. Як вже було сказано, в задачах лінійного програмування цільова функція є лінійною і в системі обмежень рівняння і нерівності також є лінійними, тобто всі невідомі входять до них в першій степені. Сформулюємо загальну задачу лінійного програмування: знайти сукупність значень
і умовам невід’ємності:
для яких лінійна функція
досягає екстремуму.
Окремі види математичної моделі задач лінійного програмування. Симетрична форма математичної моделі задач лінійного програмування. 1.
2.
Канонічна форми математичної моделі задач лінійного програмування.
Перетворення однієї форми запису в іншу. Лема. Будь-яку задачу ЛП можна звести до канонічної форми. Доведення. Математична модель будь-якої задачі ЛП складається з двох частин: системи обмежень і оптимізуючої форми. У системі обмежень окремі обмеження можуть бути двох типів: рівняння або нерівності. Покажемо, що будь-яку нерівність, введенням додаткової невідомої можна звести до рівності. Дійсно, нехай деяке обмеження має вигляд
Перепишемо його таким чином:
Введемо позначення За побудовою
Отже, обмеження-нерівність (7) і обмеження-рівність (8) є еквівалентними, тобто рівнозначними. Щоб перейти від (8) до (7), досить згадати, що  Якщо в системі обмежень є декілька нерівностей, то треба ввести відповідне число додаткових невідомих. Лему доведено. Зауваження 1. Нові додаткові невідомі треба додавати до менших частин нерівностей, бо у протилежному випадку вони не будуть невід’ємними величинами. А це одна з вимог канонічної форми ЗЛП. Зауваження 2. З метою уніфікації нові невідомі позначають
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 217. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
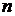 змінних
змінних  ,
,  , ...,
, ...,  , що задовольняють системі обмежень:
, що задовольняють системі обмежень: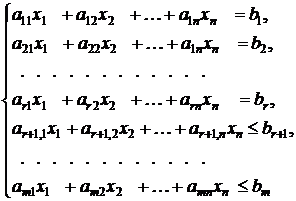
 ,
,  , ...,
, ...,  (
(  ),
),



 (7)
(7)

 є невідомою величиною. Крім того, останнє співвідношення є рівнянням відносно невідомих
є невідомою величиною. Крім того, останнє співвідношення є рівнянням відносно невідомих 
 (8)
(8) і так далі.
і так далі.