Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лема 2. Канонічна форма ЗЛП завжди може бути зведена до симетричної форми ЗЛП.Доведення. Припустимо, що невідомі
Всі невідомі (9) невід’ємні, тому
Враховуючи це, поставимо у відповідність (9) таку еквівалентну систему нерівностей:
Введемо позначення
Очевидно, що остання система обмежень збігається з (3) і рівносильна системі обмежень (5) у тому розумінні, що вони мають однакові розв’язки Для закінчення доведення леми нагадаємо, що коли замість базисних невідомих Зауваження 3. Якщо в системі обмежень є рівності і нерівності, то звести таку задачу лінійного програмування до симетричної форми можна двома шляхами: 1) спочатку звести її до канонічної форми, а потім до симетричної; 2) виділити окремою групою рівності і звести їх до нерівностей за допомогою методу, описаному в лемі 2, підставити замість базисних невідомих знайдені значення в інші нерівності і оптимізуючу форму. Із лем 1, 2 випливає така теорема. Теорема 1. Канонічна і симетрична форми еквівалентні між собою. Зауваження 4. Симетрична форма ЗЛП, рівносильна канонічній формі ЗЛП, може мати різні вигляди. Все залежить від того, які невідомі вибрати за базисні, а які – за вільні.
Різні форми задачі лінійного програмування можуть бути приведені одна до іншої за допомогою наступних зауважень.  1. На практиці інколи зустрічаються задачі, коли на змінні накладаються обмеження знизу 2. Форму можна оптимізувати або на максимум, або на мінімум. Очевидно, що коли в точці 3. Неравенства вида 4. Равенство
5. Каждое неравенство вида
добавлением неотрицательной переменной
( Пример. Привести к канонической форме задачу:
при ограничениях
Решение. Третье неравенство системы ограничений умножим на (–1) (чтобы изменить знак неравенства), а затем во второе и третье неравенства введем неотрицательные балансовые переменные
Заменим переменные
при ограничениях
Геометрична інтерпретація лінійних нерівностей та їх систем. Розглянемо в загальному виді задачу лінійного програмування для функції двох змінних: |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 242. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 є вільними, а
є вільними, а  – базисними, ранг матриці системи обмежень (5) дорівнює
– базисними, ранг матриці системи обмежень (5) дорівнює  . Розв’яжемо систему рівнянь (5) відносно базисних невідомих і нехай розв’язок має вигляд
. Розв’яжемо систему рівнянь (5) відносно базисних невідомих і нехай розв’язок має вигляд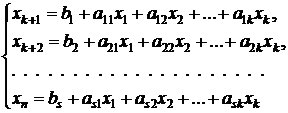 (9)
(9)
 (10)
(10) , і перепишемо (10) у вигляді
, і перепишемо (10) у вигляді
 підставити їхні значення (9) у форму (6) і згрупувати подібні члени, то вона набуде вигляду (4). Лему доведено.
підставити їхні значення (9) у форму (6) і згрупувати подібні члени, то вона набуде вигляду (4). Лему доведено. . Цю складність легко обійти, вводячи нові змінні
. Цю складність легко обійти, вводячи нові змінні 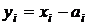 . Очевидно, що
. Очевидно, що  . В нових змінних ми вже маємо справу з задачею типу (3), (4) чи (5), (6).
. В нових змінних ми вже маємо справу з задачею типу (3), (4) чи (5), (6). функція
функція  досягає максимуму, то
досягає максимуму, то  в точці
в точці  , для неї дістанемо оптимізацію на мінімум.
, для неї дістанемо оптимізацію на мінімум. , которые могут встретиться в системе ограничений, можно привести к неравенству
, которые могут встретиться в системе ограничений, можно привести к неравенству 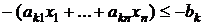 умножением на (–1).
умножением на (–1). можно заменить системой неравенств
можно заменить системой неравенств
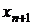 , приводится к уравнению
, приводится к уравнению (12)
(12)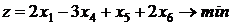

 и
и 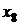 . Получим
. Получим
 и
и 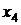 , которые не подчинены условию неотрицательности, разностью неотрицательных переменных
, которые не подчинены условию неотрицательности, разностью неотрицательных переменных  ,
,  . Наконец, вместо функции
. Наконец, вместо функции  будем рассматривать функцию
будем рассматривать функцию 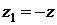 . Получим задачу
. Получим задачу