
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приклади оптимізаційних економічних задач математичного програмування.Стр 1 из 9Следующая ⇒ Предмет, метод і класифікація задач Математичного програмування. Лінійне програмування.
1. Предмет математичного програмування. 2. Приклади оптимізаційних економічних задач математичного програмування. 3. Постановка основної задачі математичного програмування. 4. Класифікація задач і методів математичного програмування. 5. Історія розвитку математичного програмування. 6. Постановка задачі лінійного програмування (ЗЛП). 7. Перетворення однієї форми запису в іншу. 8. Геометрична інтерпретація лінійних нерівностей та їх систем. 9. Геометрична інтерпретація цільової функції. 10. Випадки розв’язності задачі лінійного програмування 11. Геометричне розв’язання задачі лінійного програмування. 12. Геометричне розв’язання задач лінійного програмування у випадку, коли число змінних більше двох. 13. Геометричне розв’язання задач нелінійного програмування.
Предмет математичного програмування. В сучасній економічній науці дуже ефективно застосовуються різноманітні математичні методи дослідження. Це пов’язано з тим, що часто виникають економічні ситуації, які описуються за допомогою багатьох змінних, і які, після якісного та кількісного аналізу, можна представити у вигляді системи рівнянь та нерівностей, так званою економіко-математичною моделлю. Розв’язавши цю систему, отримаємо деякі математичні дані, які після повторного аналізу (наприклад, виключення комплексних коренів) можна застосовувати як розв’язок економічної задачі. Дуже часто в економіці ми маємо справу з екстремальними (оптимізаційними) задачами, тобто задачами, в яких потрібно знайти максимум або мінімум. Для їх розв’язку також використовуються математичні методи.  За допомогою математичних методів дослідження можуть успішно розв’язуватися такі економічні проблеми, як закономірності ціноутворення, вивчення повних затрат труда та матеріалів на одиницю продукції, дослідження міжгалузевих зв’язків, визначення рентабельності капіталовкладень, визначення ефективного розміщення виробничих сил, оптимальне планування виробничого процесу, ефективне використання обмежених ресурсів, раціональна організація технологічного процесу, обґрунтування нормативів матеріальних ресурсів та оборотних коштів та багато інших не менш важливих проблем. Одним з методів математичного дослідження є математичне програмування. Це відносно новий напрям в математиці і в даний момент активно розвивається.
Приклади оптимізаційних економічних задач математичного програмування. Приклад 1. Кондитерська фабрика для виробництва трьох видів карамелі A, B і C використовує три види основної сировини: цукровий пісок, патоку і фруктове пюре. Норми витрат сировини на виробництво однієї тонни карамелі кожного виду наведені в таблиці. В ній також вказана загальна кількість сировини кожного виду, яку може використати фабрика, а також вказано розмір прибутку від реалізації однієї тонни карамелі кожного виду.
Необхідно скласти план виробництва карамелі, який забезпечує максимальний прибуток від її реалізації. Побудуємо математичну модель задачі. Позначимо через
Визначимо тепер витрати сировини на виробництво продукції. Цукрового піску буде витрачено: Аналогічно одержимо обмеження відносно витрат патоки і фруктового пюре:
За змістом задачі величини
Приклад 2. Для нормального проходження технологічного процесу в одному з цехів хімічного заводу необхідні хімічні речовини
Яку кількість сумішей Побудуємо математичну модель задачі. Нехай
За умовою речовини
Приклад 3. Необхідно розпиляти 100 колод довжиною 6 м кожна ( Побудуємо математичну модель задачі. Можливо всього сім способів розпилу колоди. Всі відповідні дані щодо цього занесемо в таблицю:
Кількості отриманих брусків при цьому дорівнюють:
Оскільки нам необхідно одержати однакову кількість брусків кожного розміру, то повинні виконуватися такі рівності (умови комплектності):
Для виробництва максимальної кількості комплектів необхідно розпиляти всі колоди, тобто повинна виконуватися рівність (обмеження по ресурсах):
Кількість комплектів брусків визначається, наприклад, кількістю брусків довжиною 3 м:
Таким чином, одержуємо задачу максимізації цільової функції (1) при обмеженнях:
Приклад 4. Знайти найбільше і найменше значення функції за таких обмежень
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 219. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
,  і
і  заплановані обсяги виробництва (у тоннах) карамелі видів A, B і C відповідно. Тоді загальний прибуток від реалізації всієї продукції буде таким:
заплановані обсяги виробництва (у тоннах) карамелі видів A, B і C відповідно. Тоді загальний прибуток від реалізації всієї продукції буде таким: .
. тонн на виробництво карамелі виду A,
тонн на виробництво карамелі виду A,  тонн на виробництво карамелі виду B і
тонн на виробництво карамелі виду B і  тонн на виробництво карамелі виду C. Отже, загальні витрати цукрового піску складуть
тонн на виробництво карамелі виду C. Отже, загальні витрати цукрового піску складуть  тонн. Ці витрати не повинні перевищити наявних на підприємстві запасів цукрового піску (800 тонн), тобто повинна виконуватися така нерівність:
тонн. Ці витрати не повинні перевищити наявних на підприємстві запасів цукрового піску (800 тонн), тобто повинна виконуватися така нерівність:  .
. ,
, .
.
 ,
,  і
і  , місячна норма витрат яких повинна бути не менше 48, 60 і 80 кг відповідно. Ці речовини містяться в сумішах типів
, місячна норма витрат яких повинна бути не менше 48, 60 і 80 кг відповідно. Ці речовини містяться в сумішах типів 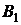 ,
, 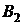 і
і  . Вміст кожної речовини
. Вміст кожної речовини  . Тоді вартість усіх закуплених сумішей буде такою:
. Тоді вартість усіх закуплених сумішей буде такою:  . Визначимо тепер кількість речовин
. Визначимо тепер кількість речовин  ,
,  ,
, 
 . Аналогічно одержуємо обмеження по кількості речовин
. Аналогічно одержуємо обмеження по кількості речовин  ,
,  . Крім того, за змістом задачі змінні
. Крім того, за змістом задачі змінні 
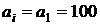 ,
,  ) на три види брусків довжиною 3 м, 2 м і 1,5 м. Визначити оптимальний план розпилу, при якому буде одержана максимальна кількість комплектів, за умови, що в комплект входить по одному бруску кожного розміру.
) на три види брусків довжиною 3 м, 2 м і 1,5 м. Визначити оптимальний план розпилу, при якому буде одержана максимальна кількість комплектів, за умови, що в комплект входить по одному бруску кожного розміру.






 ,
,
 ,
,
 .
.
 ,
, .
. .
. . (1)
. (1)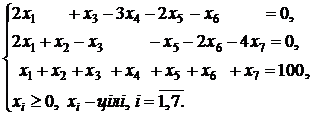 .
.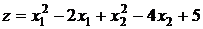
 .
.