Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Визначити найбільше (найменше) значення функції
при обмеженнях:
Відомо, що рівняння
Для визначення півплощини за відповідною нерівністю, можна скористатися і таким методом. Перетворимо початкову нерівність до виду:
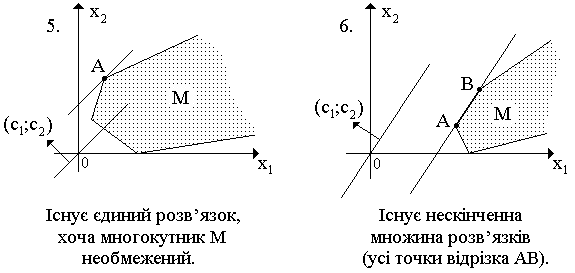
Якщо має місце перша нерівність, то відповідна множина точок знаходиться над відповідною прямою, а інакше під нею (див. малюнок). Нерівність Таким чином, кожна з нерівностей системи (2) визначає на площині Серед усіх точок многокутника M знайти таку, координати  Якої максимізують (мінімізують) функцію (1).
Геометрична інтерпретація цільової функції.
При зростанні z від –¥ до +¥ дана пряма спочатку не має спільних точок з Оскільки рух у вказаному напрямку відповідає зростанню значень z, то для точок многокутника
Випадки розв’язності задачі лінійного програмування Можливі випадки різних типів многокутників M і цільової функції для задачі максимізації функції представлені на наступних малюнках:
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 185. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) (2)
(2) , визначає в координатній площині пряму лінію. Якщо при цьому
, визначає в координатній площині пряму лінію. Якщо при цьому 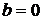 , то відповідна пряма проходить через початок координат. Кожна пряма виду
, то відповідна пряма проходить через початок координат. Кожна пряма виду 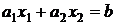 розбиває координатну площину на дві півплощини. Для точок однієї з цих півплощин виконується нерівність виду
розбиває координатну площину на дві півплощини. Для точок однієї з цих півплощин виконується нерівність виду  , а для точок другої виконується нерівність виду
, а для точок другої виконується нерівність виду  . Пряма
. Пряма  Для того, щоб визначити, у якій півплощині відносно заданої прямої виконується нерівність виду
Для того, щоб визначити, у якій півплощині відносно заданої прямої виконується нерівність виду 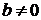 , точкою для перевірки найкраще обирати точку початку координат.
, точкою для перевірки найкраще обирати точку початку координат. , або
, або  .
. (або
(або 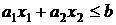 ) визначає півплощину з її граничною прямою.
) визначає півплощину з її граничною прямою. деяку півплощину. Перетин півплощин, заданих нерівностями системи (2), визначає в площині
деяку півплощину. Перетин півплощин, заданих нерівностями системи (2), визначає в площині  , який лежить у першій координатній чверті. Цей многокутник може бути і необмеженим (див. приклад 2). Виходячи з геометричного змісту обмежень (2), цю задачу можна сформулювати в такому вигляді:
, який лежить у першій координатній чверті. Цей многокутник може бути і необмеженим (див. приклад 2). Виходячи з геометричного змісту обмежень (2), цю задачу можна сформулювати в такому вигляді: Нехай
Нехай  визначає деяку пряму. При зміні z ця пряма переміщується паралельно самій собі, тому що її кутовий коефіцієнт визначається тільки числами c1 і c2 і тому залишається незмінним. Вектор
визначає деяку пряму. При зміні z ця пряма переміщується паралельно самій собі, тому що її кутовий коефіцієнт визначається тільки числами c1 і c2 і тому залишається незмінним. Вектор  є градієнтом функції z і паралельне переміщення прямої в напрямку цього вектора веде до збільшення значень цільової функції.
є градієнтом функції z і паралельне переміщення прямої в напрямку цього вектора веде до збільшення значень цільової функції.